ان المتقدمين من المهندسين، نظروا في خواص المثلث المتساوي الأضلاع، فظهر لهم، أن كل نقطة، تفرض على ضلع من أضلاع المثلث، المتساوي الأضلاع، ويخرج منها عمودان، على ضلعي المثلث الباقيين، فإن مجموعهما مساو لعمود المثلث.
فدونوا ذلك، واثبتوه في كتبهم، ونظروا في أعمدة المثلثات الباقية، فلم يجدوا لها نظاما تاما، ولا ترتيبا، فلم يذكروا فيها شيئا.
ولما كانت الحال هذه، دعتنا الحاجة إلى النظر في خواص المثلثات، فوجدنا لأعمدة المثلث المتساوي الساقين، نظاما مطردا، ووجدنا لأعمدة المثلث المختلف الأضلاع، أيضا، نظاما وترتيبا مطردا. فلما تبين لنا ذلك، ألفنا فيه هذه المقالة.
ونحن نقدم أولاً، ما ذكره المقدمون، من خاصة أعمدة المثلث المتساوي الأضلاع، ثم نتبعه بما استخرجناه نحن، من خواص أعمدة المثلثات الباقية، لتكون خواص أعمدة جميع المثلثات، مجتمعة في هذه المقالة.
أما الذي ذكره المتقدمون، فهو:
١ - كل مثلث متساوي الأضلاع، تفرض على أحد أضلاعه نقطة، ويخرج منها عمودان إلى الضلعين الباقين، فإن مجموعهما مساو لعمود المثلث.
مثال ذلك، مثلث أ ب ج، متساوي الأضلاع، وفرض على ضلع ا ب نقطةد ، وأخرج منها عمودا د ه د ز، وأخرج عمود ا ح، فإن عمودي د ه د ز، مساويان بمجموعهما لعمود ا ح .
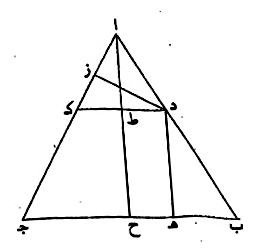
برهان ذلك، أنا نخرج من نقطة د، خطاً موازيا، لخط ب ج، وليكن د ط ك.
فيكون مثلث، ا د ك، متساوي الأضلاع، لأنه شبيه بمثلث ا ب ج .
فيكون عمود د ز، مثل عمود ا ط، وعمود د ه، مثل عمود ط ح، فعمودا د ه د ز مثل عمود ا ح، وذلك هو المراد.
وذكر المتقدمون أيضا،
٢ - أن كل مثلث متساوي الأضلاع، يُفرَضُ في داخله نقطة، وخُرِّجَ منها أعمدة إلى أضلاع المثلث، فإن مجموع تلك الأعمدة، مساو لعمود المثلث.
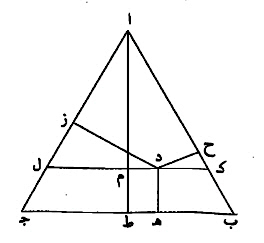
مثال ذلك، مثلث ا ب ج، متساوي الأضلاع، وفرض في داخله نقطة د.
خرج منها أعمدة د ه د ز د ح، وخرج عمود ا ط.
فان أعمدة، د ه د ز د ح مجموعة، مثل عمود ا ط.
برهان ذلك، أنا نخرج، من نقطة د، خطا موازيا، لخط ب ج، وليكن ك م ل.
يكون مثلث ا ك ل، متساوي الأضلاع.
يكون عمودا د ح د ز، مساويين بمجموعهما لعمود ا م، كما تقدم.
ويكون عمود د ه مثل م ط.
فمجموع أعمدة د ه د ز د ح، مثل عمود ا ط.
هذا ما ذكره المتقدمون، في هذا المعنى، وأما الذي استخرجناه نحن، فهو الذي نذكره الآن:
أ - كل مثلث، يخرج من زواياه، أعمدة على اضلاعه، فإن نسبة العمود إلى العمود، كنسبة الضلع إلى الضلع، بالتكافئ.
مثال ذلك، مثلث ا ب ج، خرج فيه أعمدة، ا د ب ه ج ز.
فأقول، إن نسبة عمود ا د، إلى عمود ب ه، كنسبة ج ا، الى ج ب، وان نسبة عمود ا د، الى ج ز، كنسبة ب ا الى ب ج.
برهان ذلك، ان زاويتي، د ه، كل واحدة منها قائمة، وزاوية ا ج د مشتركة، فمثلث ا ج د شبيه بمثلث ب ج ه.
نسبة عمود ا د، إلى عمود ب ه، كنسبة ج ا، الى ج ب.
كذلك نبين، ان نسبة عمود ا د، الى ج ز، كنسبة ب ا الى ب ج.
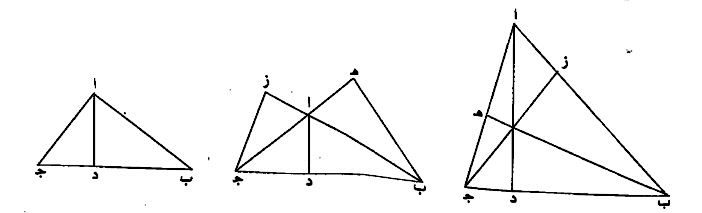
فاذا كان المثلث حاد الزوايا، فمساقط الأعمدة، تكون ثلاثتها في داخل المثلث، على ما في الصورة الأولى.
وان كان المثلث، منفرج الزاوية، فواحد من الأعمدة، يكون في داخل المثلث، والعمودان الباقيان، يكونان خارج المثلث، على ما في الصورة الثانية.
وإن كان المثلث قائم الزاوية، فالعمودان الخارجان من الزاويتين الحادتين، إنما هما، ضلع المثلث، المحيطان بالزاوية القائمة، فمسقطا العمودين، اللذين هما ز ه، يكونان عند نقطة ا، على ما في الصورة الثالثة.
ونبين هذا الشكل، ببرهان آخر، وهو أن ضرب كل ضلع، في العمود الواقع عليه، هو ضعف المثلث.
فنسبة، كل واحد من أضلاع المثلث، إلى ضلع غيره، هي نسبة العمود، الواقع على الضلع الثاني، إلى العمود الواقع على الضلع الأول، وذلك ما أردنا بيانه.
ب - وأيضا، فإن كل مثلث، قائم الزاوية، مختلف الأضلاع، يخرج من زاويته القائمة، عمود على القاعدة، ثم يفصل، من أعظم قسمي القاعدة، مثل أصغرهما، ويوصل بين نهايته، وبين الزاوية القائمة بخط، ثم تقسم الزاوية، التي تبقى من الزاوية القائمة، بنصفين، فإن الجزء، الذي ينفصل من القاعدة، بين الخط، الذي يقسم الزاوية الباقية، وبين مسقط العمود، مساو للعمود.
مثال ذلك، مثلث ا ب ج، زاوية ا منه قائمة.
خرج منها عمود ا د، وفصل د ه مثل د ج.
وصل ا ه، وقسمت زاوية، ب ا ه بنصفين، بخط ا ز.
فأقول، إن ز د مثل د ا.
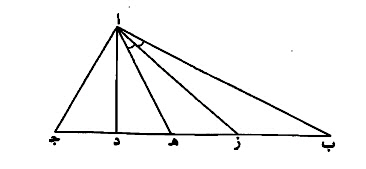
برهان ذلك، أن زاوية ه ا د، مثل زاوية د ا ج.
فزاوية، ه ا د، نصف زاوية ه ا ج.
وزاوية، ه ا ز نصف زاوية ه ا ب.
فزاوية ز ا د نصف زاوية ب ا ج.
زاوية ب ا ج قائمة، فزاوية ز ا د نصف قائمة.
زاوية ا د ز قائمة، فزاوية ا ز د نصف قائمة.
خط ز د مثل خط د ا، وذلك ما أردنا بيانه.
ج - كل مثلث، متساوي الساقين، يُفرَضُ على قاعدته نقطة، كيفما اتفقت، ويخرج عمودان على ضلعي المثلث، فإن مجموعهما، مساو للعمود، الخارج من طرف القاعدة على ضلع المثلث. اكانت زاوية المثلث، التي يحيط بها الضلعان المتساويان، حادة، أو منفرج او قائمة.
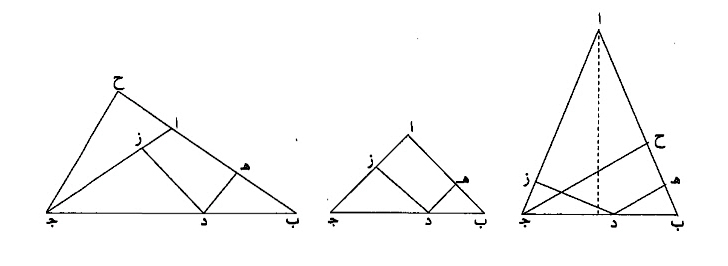
مثال ذلك، مثلث ا ب ج متساوي الساقين، ضلعا ا ج ب ا منه متساويان، وقاعدته ب ج.
فرض على قاعدة ب ج نقطة د، وخرج منها عمودا د ه د ز.
فأقول، إنهما مساويان بمجموعهما، لعمود ج ح.
برهان ذلك:
أن زاويتي ب ج متساويتان.
زاويتي ه ز متساويتان لانهما قائمتان.
فمثلثا ب ه د د ز ج متشابهان.
فنسبة ج د إلى د ب، كنسبة د ز إلى د ه .
وبالتركيب، نسبة ج ب إلى د ب، كنسبة د ز د ه مجموعين، إلى د ه.
ونسبة ج ب إلى د ب، كنسبة ح ج إلى د ه.
فنسبة د ز د ه مجموعين، إلى د ه، كنسبة ج ح إلى د ه.
فعمودا د ز د ه مجموعان، مساويان لعمود ج ح.
وهذا البرهان مطرد في صفة المثلث، وهو المراد.
د -
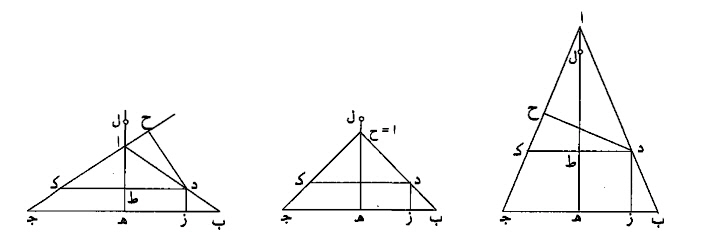
وأيضا، فإنا نعيد الصورة، والنقطة المفروضة على ضلع ا ب، ولتكن د.
نخرج منها عمودي د ز د ح.
نخرج عمود ا ه، ونجعل نسبةا ه إلى ط ه ، كنسبة ا ب إلى د ب.
نجعل نسبة ا ط إلى ل ط ، كنسبة ا ج إلى ج ب.
فأقول: إن عمودي د ز د ح، مثل عمود ل ه.
برهان ذلك:
انا نصل د ط وننفذه الى ك.
فيكون د ك موازيا لخط ب ج.
ولان نسبة، ا ه، الى ط ه، كنسبة ا ب، الى د ب، فتكون نسبة ا ج الى ج ب، كنسبة ا ك الى ك د.
نسبة ا ج الى ج ب، هي كنسبة ا ط، الى ل ط.
فنسبة ا ك الى ك د، كنسبة ا ط، الى ل ط.
ونسبة ا ك الى ك د، هي كنسبة ا ط الى ح د، كما تبين في ج.
فعمود ل ط مثل ح د، و د ط مثل ط ه.
فعمودا د ز د ح مثل عامود ل ه.
وذلك ما اردنا ان نبينه.
ه -
أيضا، فإنا نعيد المثلث المتساوي الساقين، ولتكن النقطة في داخل المثلث.
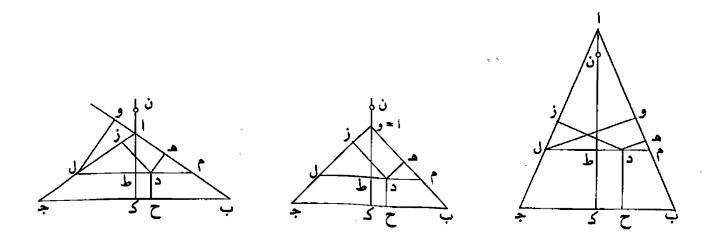
ليكن المثلث، ا ب ج، والنقطة د، وهي في داخل المثلث.
لنخرج منها اعمدة د ه د ز د ح، ونخرج من نقطة د، خطاً موازيا لخط ب ج، وليكن م د ل.
ونخرج عمود ا ط ك، ونجعل نسبة، ا ط الى ن ط، كنسبة ا ب الى ب ج، التي هي نسبة، ا م الى م ل.
فأقول، إن أعمدة د ه د ز د ح، مجموعة، مثل عمود ن ك.
برهان ذلك:
أنا نخرج عمود ل و.
فلأن نسبة، ا ط إلى ن ط كنسبة ا م إلى م ل، يكون ن ط مثل ل و، كما تقدم.
وقد تبين، أن عمودي، د ه د ز مجموعين، مثل عمود ل و.
وعمودا د ه د ز مثل عمود ن ط.
وعمود د ح مثل عمود ط ك.
فمجموع أعمدة، د ه د ز د ح الثلاثة مساو لعمود ن ك.
وذلك ما أردنا بيانه.
وهذا البرهان مطرد في جميع المثلثات المتساوية الساقين، الحاد منها، والمنفرج، والقائم.
و -
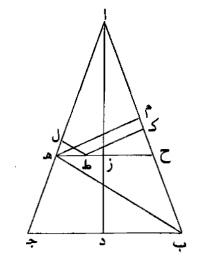
وأيضا، فإنا نعيد المثلث المتساوي الساقين، وليكن مثلث ا ب ج، ونقسم زاوية ا ب ج منه، بنصفين، بخط ب ه، ونخرج ه ح موازيا لقاعدة ب ج، ونخرج عمود ا ز د.
فأقول، إن كل نقطة تفرض، على خط ه ح ويخرج منها عمودان، على خطي، ا ه ا ح، فإنهما مجموعان، مساويان لعمود ز د.
نفرض على خط ه ح، نقطة ط ، ونخرج منها عمودي، ط ك ط ل، فأقول، إن ط ك ط ل، مجموعين، مساويان لعمود ز د.
برهان ذلك:
انا نخرج عمود ه م.
ح ه، مواز لخط ب ج .
تكون زاوية ح ه ب، مساوية لزاوية ج ب ه .
زاوية ج ب ه، مساوية لزاوية ح ب ه .
فزاوية ح ه ب مساوية لزاوية ح ب ه.
فخط ح ه مثل خط ح ب.
فنسبة ح ا الى ح ب، هي نسبة ح ا الى ح ه.
نسبة ح ا الى ح ب، هي نسبة ز ا الى ز د.
نسبة ح ا الى ح ه، هي نسبة عمود ز ا الى عمود م ه، كما تقدم.
نسبة ز ا الى ز د، هي نسبة ز ا الى م ه.
فعمود م ه، مثل ز د.
عمود م ه، هو مثل عمودي، ط ك ط ل، كما تقدم.
فعمودا ط ك ط ل مجموعين، مثل عمود ز د .
وهذا البرهان مطرد، في جميع المثلثات، المتساوية الساقين.
ز - كل مثلث، متساوي الساقين، حاد الزوايا، فان زيادة ضلعه، الذي هو أحد ساقيه، على عموده، الذي يقع على ذلك الضلع، وزيادة العمود على مسقط حجره، وضعف مسقط الحجر، الثلاثة، متوالية على نسبة واحدة.
فليكن، مثلث ا ب ج، متساوي ساقي، ا ب ا ج، وزواياه الثلاث حادة، وليخرج فيه عمود ج ه.
فأقول، إن زيادة ا ب، على ج ه، وزيادة ج ه، على ه ب، وضعف ه ب، الثلاثة، متوالية على نسبة واحدة.
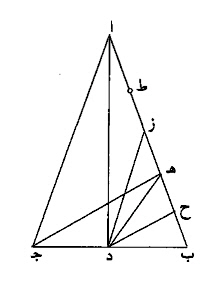
برهان ذلك:
انا نخرج عمود ا د وعمود د ح، مما يجعل ح ه مثل ح ب.
نصل ه د.
نقسم زاوية ا د ه، بنصفين، بخط د ز.
فيكون ز ح مثل ح د، كما تبين في د من هذه المقالة.
فلأن ج ب ضعف د ب، و ه ب ضعف ح ب، يكون ج ه، موازيا ل د ح، ويكون ج ه، ضعف د ح.
فيكون ج ه، عمودا على ا ب.
ولأن ضرب ا ح، في ح ب، مثل مربع ح د، يكون ضرب ا ح، في ح ه، مثل مربع ح ز.
فنسبة ا ح، إلى ح ز كنسبة ح ز، إلى ح ه، وكنسبة ا ز، إلى ز ه.
و ح ز، أعظم من ح ه، لأن ح ز أعظم من ح ب.
وذلك أن ا د، أعظم من د ب، لأن زاوية ب ا ج، حادة، فخط ا ز، أعظم من خط ز ه.
فنجعل ز ط مثل ز ه، فتكون نسبة ا ز، إلى ز ط، كنسبة ز ح إلى ح ه.
فنسبة ا ط، إلى ط ز، كنسبة ز ه، إلى ه ح.
فضرب ا ط، في ح ه، مثل مربع ز ه.
فضرب ا ط، في ح ب مرتين، مثل ضعف مربع ه ز.
فضرب ا ط، في ب ه مرتين، مساو لمربع ه ط، نسبة واحدة.
ولأن ز ه، مثل ز ط، و ه ح، مثل ح ب، يكون ط ب ضعف ح ز.
و ح ز مثل ح د، و ج ه ضعف ح د، فخط ط ب، مثل عمود ج ه، ف ا ط هو زيادة ا ب على عمود ج ه.
و ط ب، هو مثل عمود ج ه، و ط ه هو زيادة ط ب على ه ب.
و ا ط، و ط ه، و ضعف ه ب، الذي هو مسقط الحجر لعمود ج ه، متوالية على نسبة، فزيادة ا ب، على عمود ج ه، و زيادة عمود ج ه، على ه ب، الذي هو مسقطه، و ضعف ه ب،الثلاثة، متوالية على نسبة واحدة، و ذلك ما اردن بيانه.
ح -
وأيضا، فليكن مثلث ا ب ج، مختلف الاضلاع، ولنفرض على ضلع من اضلاعه، أي ضلع كان، نقطة.
لتكن نقطة د. نخرج من نقطة د، عمودي د ه د ز. نخرج عمود ب ح. نخرج د ك ط، موازيا لخط ا ج. نجعل نسبة ب ك، الى ن ك، كنسبة ب ج، الى ج ا.
أقول، ان عمودي د ه د ز، مساويان، لعمود ن ح.
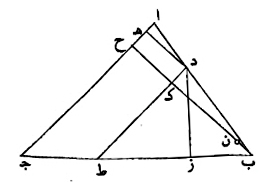
برهان ذلك، ان:
نسبة ب ج الى ج ا، كنسبة ب ط الى ط د.
نسبة ب ج الى ج ا، كنسبة ب ك الى ن ك.
فنسبة ب ط الى ط د، كنسبة ب ك الى ن ك.
نسبة ب ط الى ط د، كنسبة ب ك الى ز د.
فعمود ز د مثل عامود ن ك، وعمود د ه مثل عامود ك ح.
فعمودا د ز د ه مجموعين، مثل عامود ن ح، وذلك ما اردنا بيانه.
ط -
ولنعد، المثلث المختلف الأضلاع، وليكن ا ب ج. نفرض في داخله نقطة د، كيفما اتفق. نخرج منها أعمدة د ه د ز د ح. نجيز على نقطة د، خطا موازيا لخط ب ج، وليكن ل د م. نخرج عمود ا ط ك، ونجعل نسبة ا ط، إلى ن ط، كنسبة ب ج، الى ج ا.
فأقول، إن مجموع أعمدة د ه د ز د ح الثلاثة، مساو لعمود ن ك.
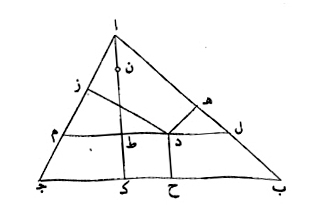
برهان ذلك، أن:
نسبة ب ج إلى ج ا، كنسبة ل م الى م ا.
نسبة ب ج إلى ج ا، كنسبة ا ط إلى ن ط.
فنسبة ا ط الى ن ط، كنسبة ل م إلى م ا.
عمودا د ه د ز، مساويان لعمود ن ط، كما تبين فيما تقدم.
وعمود د ح، مثل عمود ط ك.
فمجموع أعمدة د ه د ز د ح، مساو لعمود ن ك.
وهذا البرهان، مطرد في جميع المثلثات القائمة، والحادة، والمنفرجة، المختلف الأضلاع، والمتساوي الساقين، والمتساوي الأضلاع، وذلك ما أردنا ان نبين.
تمت المقالة في اعمدة المثلثات، ولله الحمد، وفرغت من كتابتها بالموصل، في صفر سنة ٦٣٢ بعد الهجرة.