في استخراج الأعداد المتحابة، ثابت بن قرة

الأعداد المتحابة، فإنها الاعداد، التي إذا جمع كل جزء، لكل واحد منها، على حدة، كانت جملة ذلك مثل العدد الآخر.

مثلا، عدد 220، اجزائه هي، مع الواحد، 1 و2 و4 و5 و10 و11 و20 و22 و44 و55 و110، وجمعها هو 284.

وعدد 284 اجزائه هي، مع الواحد، 1 و2 و4 و71 و142 ومجموعها هو 220.

إذا، 220 و284 عددان متحابان.

بَيَّنَ ثابت بن قرة، كيفية اجاد اعداد متحابة، كم شئنا، وذلك عبر استخراج أولا، ثلاث اعداد أولية، ومنها استخراج عددين متحابين.

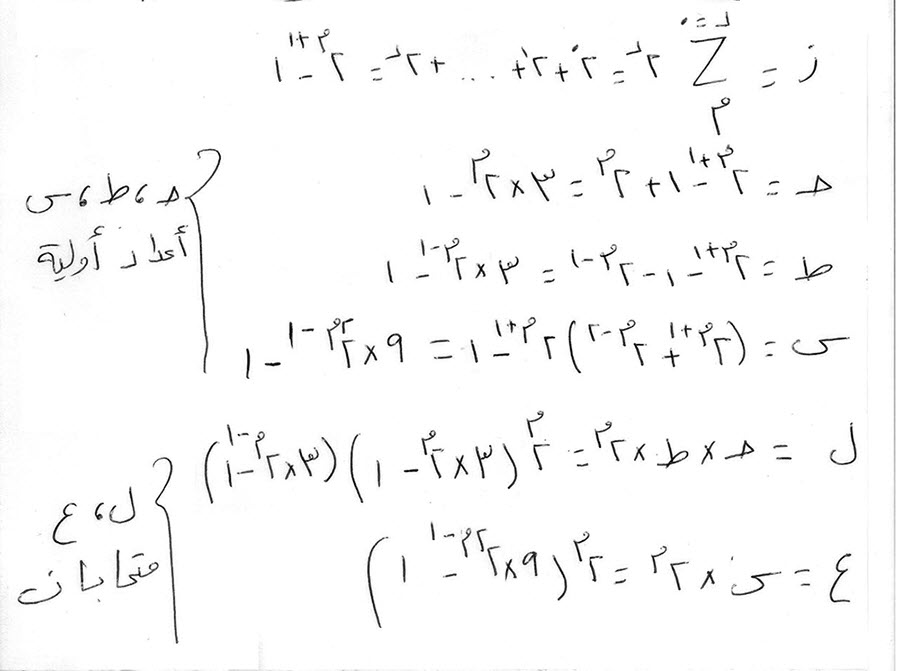
مثال على ذلك:

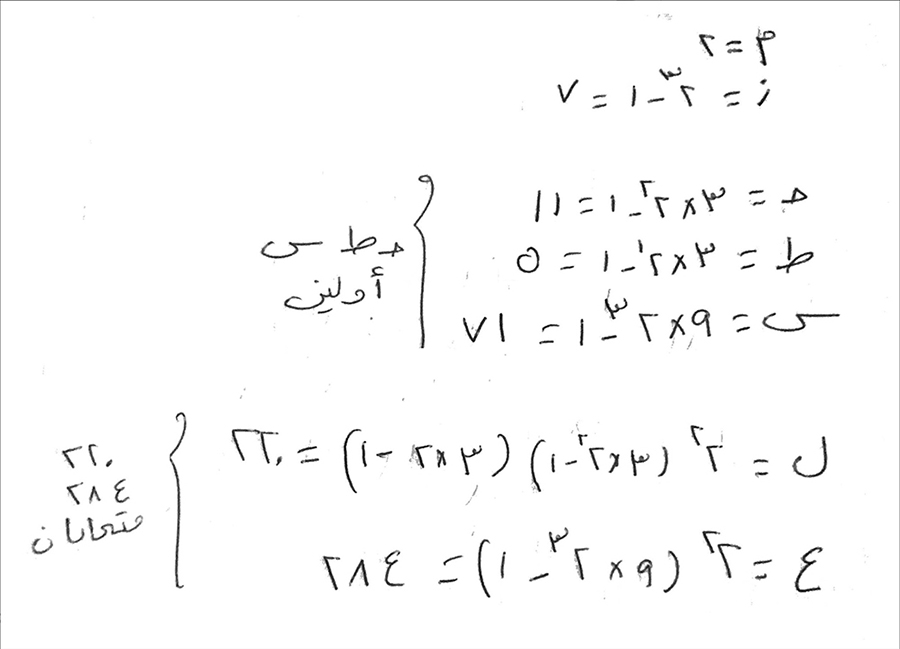
وبين ثابت ذلك بما يلي:

ي - نريد أن نبين، كيف نجد أعداداً متحابة كم شئنا.

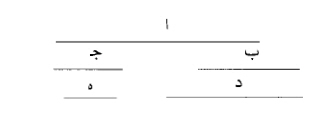
نضع أعداداً متوالية، على نسبة الضعف من الواحد، ومعها الواحد يقدمها.

لتكن أعداد أ ب ج د ه.

لتكن جملة، أ ب ج د ه، إذا جمعت عدد ز.

نزيد على عدد ز، آخر الأعداد التي جمعت، وهو عدد ه، لتكن جملتها عدد ح.

ننقص من عدد ز، ما يلي عدد ه قبله، وهو عدد د، وليكن الباقي عدد ط.

إن كان، كل واحد من عددي ح ط، عدداً أولاً غير عدد الاثنين، فهو الذي نريد.

ان لم يكن، تجاوزنا الأعداد التي جمعت إلى غيرها، حتى ننتهي إلى ما يكون هذان العددان منه، عددين أولين.

ليكن عددا ح ط أولين، وليس واحد منهما عدد الاثنين.

نضرب أحدهما في الآخر، وليكن المجتمع من ذلك عدد ك.

نضرب عدد ك، في آخر الأعداد، التي كانت جمعت، وهو عدد ه، وليكن المجتمع من ذلك عدد ل، فيكون هذا عدداً واحداً، نقف عليه ونحفظه.

نجمع العدد الذي يتلو عدد ه، من الأعداد التي أخذت على نسبة الضعف، وهو عدد و، مع ما قبل آخر الأعداد، التي جمعت بواحد، وهو عدد ج، وليكن جميعهما عدد م.

ليكن المجتمع، من ضرب عدد م، في عدد و، عدد ن .

ننقص منه واحد، ونجعل الباقي عدد س.

إن كان عدد س عدداً أولاً، فهو الذي نريد.

إن لم يكن، تجاوزنا الأعداد التي جمعت، حتى ننتهي إلى ما يصير هذا العدد، والأعداد التي تقدم ذكرها كل واحد منها، عدداً أولا.

فليكن س عدداً أولاً.

نضربه في عدد ه، وليكن المجتمع من ذلك، عدد ع .

أقول، إن عددي ل ع، عددان متحابان.

برهان ذلك:

جمعت اعداد متوالية على نسبة الضعف، من الواحد، والواحد معها، وهي أ ب ج د ه، وكانت جملتها عدد ز.

ضرب في العدد الأكثر، من الأعداد التي جمعت، وهو عدد ه، عدد آخر من الأعداد الأول، وهو عدد س، وهو أكثر من عدد ز، فاجتمع من ذلك عدد ع، فعدد ع عدد ناقص، ومبلغ نقصانه، مثل زيادة عدد س، على عدد ز. (٥، أعداد تامة)

إذا جعلنا هذه الزيادة عدد ف، صار عددا ف ز مجموعين، مثل عدد س.

عدد ن، يزيد على عدد س، واحداً، فعددا ف ز، مجموعين مع الواحد، مثل عدد ن.

عدد ن، قد كان مجتمعاً، من ضرب عدد و، في عدد م.

عددا ف ز، مجموعين مع الواحد، مثل ما يجتمع من ضرب عدد و، في عدد م.

عدد م، قد كنا جعلناه، مثل عددي و ج مجموعين.

عددا ف ز مع الواحد، مثل المسطح الكائن، من ضرب عدد و، في عددي و ج.

عدد ز مع الواحد، مثل عدد و . (د، أعداد متوالية)

عددا ف و مجموعان، مثل المسطح الكائن، من ضرب، عدد و، في عددي و ج مجموعان.

إذا أسقطنا منهما جميعاً عدد و، كان الباقي، وهو عدد ف، مثل الباقي، وهو المسطح، الكائن من ضرب عدد و، في عددي و ج مجموعين غير واحد.

عددي و ج مجموعان غير واحد، مثل عددي ز ج مجموعين، لأن و يزيد على ز واحداً.

عدد ف، مثل المسطح الكائن من ضرب عدد و، في عددي ز ج مجموعين.

ايضا، فإنه قد جمعت، اعداد متوالية على نسبة الضعف، مبتدئة من الواحد، والواحد فيها، وهي أعداد أ ب ج د ه، فكانت جملتها عدد ز.

عدد ل اجتمع من، ضرب في العدد الأكثر، من الأعداد التي جمعت، وهو عدد ه، عدد ك، وهو عدد مسطح، ضلعاه عددان أولان مختلفان غير الاثنين وهما ح ط.

عدد ك المسطح، أقل، من المجتمع من ضرب عددي ح ط مجموعين، في عدد ز .

عدد ل إذا، عدد زائد. (و، أعداد تامة)

مبلغ زيادة عدد ل، مثل المجتمع من ضرب عدد ط في عدد ز، مزيداً على ذلك عدد ز، مزيداً على ذلك ضرب عدد ح، في العدد الحاصل من ز ناقص ط.

نجعل جملة هذه الزيادة، التي ذكرنا، عدد ص.

عدد ط، هو مثل عدد ز منقوصاً منه عدد د.

عدد ح، فهو مثل عددي ز ه مجموعين.

عدد ز منقوصا من عدد ط، مثل عدد د .

عدد ص، يكون مثل المجتمع، من ضرب عدد ز منقوصاً منه عدد د، في عدد ز، مزيداً على ذلك عدد ز، مزيداً على ذلك ضرب عددي ز ه مجموعين، في عدد د.

ذلك هو مثل المجتمع من ضرب عدد ز في نفسه، مزيداً على ذلك عدد ز، مزيداً على ذلك ضرب عدد ه في عدد د.

لكن، المجتمع من ضرب عدد ه، في عدد د، مثل المجتمع من ضرب عدد و، في عدد ج، لأن أعداد، ج د ه و، الأربعة متناسبة.

عدد ص، مثل المجتمع من ضرب عدد ز في نفسه، مزيداً على ذلك عدد ز، مزيداً على ذلك ضرب عدد و، في عدد ج .

لكن، عدد ز مع المجتمع من ضرب عدد ز في نفسه، مثل المجتمع، من ضرب عدد ز وزيادة واحد، في عدد ز.

عدد ص، مثل المجتمع من ضرب عدد ز وزيادة واحد، في عدد ز، مع المجتمع من ضرب عدد و في عدد ج.

عدد ز مع الواحد مثل عدد و.

عدد ص، مثل المجتمع من ضرب عدد و، في عدد ز، ومن ضرب عدد و في عدد ج.

عدد ص إذا، مثل المسطح الكائن من ضرب عدد و، في عددي ز ج مجموعين.

أيضاً، فإن عدد ل، مجتمع من ضرب عدد ك، في عدد ه.

عدد ع، مجتمع من ضرب عدد ه في عدد س.

إذا جعلنا عدد ق، فضل ما بين عددي ع ل، كان عدد ق، مثل المجتمع من ضرب عدد ه، في فضل ما بين عددي س ك.

عدد س مثل عدد ن منقوصاً منه واحد.

عدد ك، فقد كان مجتمعا، من ضرب عدد ح في عدد ط.

عدد ح مثل عددي ه ز مجموعين.

عدد ط مثل عدد ز ناقص عدد د.

فيكون عدد ق، مثل المجتمع من ضرب عدد ه، في فضل ما بين، عدد ن غير واحد، وبين المسطح الكائن من ضرب، عددي ز ه مجموعين، في عدد ز منقوصا منه د.

عدد ن، قد كان مجتمعاً من ضرب عدد و، في عدد م.

يكون عدد ق، مثل المجتمع من ضرب عدد ه، في فضل ما بين، المسطح الكائن من ضرب عدد و في عدد م منقوصا من هذا المسطح واحد، وبين المسطح الكائن من ضرب، عددي ز ه مجموعين، في عدد ز منقوصا من د.

عدد م، هو مثل عددي و ج مجموعين.

عدد و، يزيد على عدد ز واحداً.

عددا ز ه مجموعان، هما مثل عددي و ه مجموعان غير واحد.

عدد ز ناقص عدد د، مثل عدد و غير واحد ناقص عدد د .

يكون عدد ق، مثل المجتمع من ضرب عدد ه، في فضل ما بين، المسطح الكائن من ضرب عدد و في عددي و ج مجموعين، منقوصا من هذا المسطح واحد، وبين المسطح الكائن، من ضرب عددي و ه مجموعان غير واحد، في عدد و غير واحد غير عدد د.

عدد و غير واحد غير عدد د، مثل عددي د ه مجموعان غير واحد، لأن أعداد د ه و، متوالية على نسبة الضعف. (د، أعداد متوالية)

فيكون عدد ق، مثل المجتمع من ضرب عدد ه، في فضل ما بين، المسطح الكان من ضرب عدد و في عددي و ج مجموعين، منقوصا من هذا المسطح واحد، وبين المسطح الكائن، من ضرب عددي و ه مجموعين غير واحد، في عددي د ه مجموعان غير واحد .

المجتمع، من ضرب عدد ه، في فضل ما بين، المسطح الكان من ضرب عدد و في عددي و ج مجموعين، منقوصا من هذا المسطح واحد، وبين المسطح الكائن، من ضرب عددي و ه مجموعين غير واحد، في عددي د ه مجموعان غير واحد، مثل المسطح الكائن، من ضرب عدد و، في عددي و ج مجموعين غير واحد، لأن أعداد ج د ه و متوالية على نسبة الضعف. (ط، أعداد متوالية)

فيكون عدد ق، مثل المسطح الكائن، من ضرب عدد و، في عددي و ج مجموعان غير واحد.

عددي، و ج مجموعان غير واحد، مثل عددي ز ج مجموعان، لأن عدد و، يزيد على عدد ز واحداً.

عدد ق، مثل المسطح الكائن، من ضرب عدد و، في عددي ز ج مجموعين.

كنا قد بينا، أن كل واحد من عددي ف ص، أيضا مثل المسطح الكائن، من ضرب عدد و، في عددي ز ج مجموعين.

أعداد ف ص ق الثلاثة متساوية.

عدد ف منها، بينا أنه مثل نقصان كل جزء، لعدد ع الناقص، إذا جمع ذلك عليه كله.

عدد ق، فهو نقصان عدد ل، عن عدد ع، فعدد ل إذاً، مساو لكل جزء لعدد ع، إذا جمع.

أيضا، فإن عدد ص، قد بينا، أنه مثل زيادة كل جزء، لعدد ل الزائد، إذا جمع ذلك كله عليه.

عدد ق، هو زيادة عدد ع، على عدد ل، فعدد ع إذا مساو لكل جزء لعدد ل إذا جمع.

عدد ل، مساو لكل جزء لعدد ع إذا جمع، فعددا ل ع متحابان، وذلك ما أردنا أن نبين.

وهو بيِّن مماً وصفنا، أن كل عددين مقترنين من الأعداد المتحابة، فإن أحدهما عدد زائد، وهو أقلهما، والآخر عدد ناقص، وهو أكثرهما، وأن زيادة الزائد منهما، مثل نقصان الناقص، وإن ذلك يكون بمثل فضل ما بين العددين أنفسهما، وإنه إذا أخذ كل جزء، لكل واحد منهما، وجمع ذلك كله معا، كانت جملة ذلك، مثل ذينك العددين مجموعين.