بسم الله الرحمن الرحيم، وما توفيقي إلا بالله،
نقل، اسحق بن حنين، إصلاح، ثابت بن قرة، وهو، ثمانية وأربعون شكلا.
١ - النقطة، هي شيء ما، لا جزء له.
٢ - الخط، هو طول، لا عرض له، ونهايتا الخط، نقطتان.
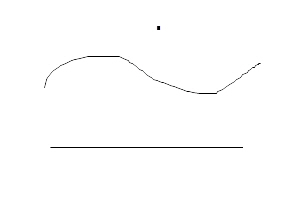
٣ - الخط المستقيم، هو، الموضوع على مقابله، ايّ النقط، كانت عليه، بعضها لبعض.
٤ - البسيط، او السطح، هو ما له، طول، وعرض، فقط، ونهايات البسيط، خطوط.

٥ - السطح المستوي، هو الموضوع، على مقابله، أي الخطوط المستقيمة، كانت عليه، بعضها لبعض.
٦ - الزاوية البسيطة، هي انحراف، كل واحد، من خطيين، موضوعين، في بسيط مستوي، متصلين، على غير استقامة، أحدهما عن الاخر.
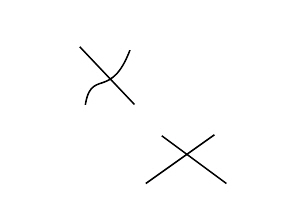
٧ - إذا كان الخطان، المحيطان، بهذه الزاوية، مستقيمين، سميت، بالزاوية المستقيمة الخطين.
٨ - إذا قام، خط مستقيم، على خط مستقيم، فصير الزاويتين، التين جنبيه، متساويتين، فكل واحدة منهما، هي زاوية قائمة، وذلك الخط القائم، يقال له عمود، على الخط، الذي هو قائم عليه.
٩ - الزاوية، التي هي أكبر، من قائمة، يقال لها، المنفرجة.
١٠ - الزاوية، التي هي أصغر، من قائمة، يقال لها، الحادة.
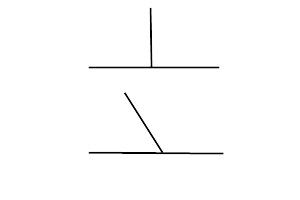
١١ - الحَدّ، هو نهاية الشيء.
١٢ - الشَكْل، ما أحاط به، حد، او حدود.
١٣ - الدائرة، هي شكل بسيط مستوي، يحيط به، خط واحد، في داخله، نقطة، كل الخطوط المستقيمة، التي تخرج منها، وتنتهي، الى ذلك الخط، مساوٍ، بعضُها البعْض، وتلك النقطة، هي مركز الدائرة.
١٤ - قطر الدائرة، هو خط مستقيم، يمرّ، بمركز الدائرة، وينتهي، في الجانبين، الى الخط المحيط بها، وهو يقطعها بنصفين.
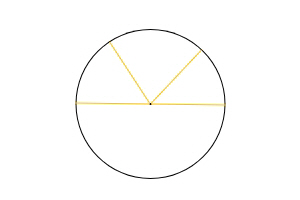
١٥ - نصف الدائرة، هو شكل، يحيط به القطر، و، القوس التي حادها القطر من الخط المحيط بها، ومركزها مركز الدائرة.
١٦ - قطعة الدائرة ، هي شكل، تحيط به، خط مستقيم، وقوس، من قطعة الدائرة، اما أكبر من نصفها، او أصغر.
١٧ - الأشكال المستقيمة الخطوط، هي التي تحيط بها، خطوط مستقيمة. فذوات، الثلاث اضلاع، هي التي يحيط بها، ثلاثة خطوط مستقيمة. وذوات، الأربعة اضلاع، هي التي تحيط بها، أربعة خطوط مستقيمة. وذوات، الاضلاع الكثيرة، فالتي تحيط بها، أكثر، من أربعة خطوط، مستقيمة.
اما الاشكال، ذوات الاضلاع الثلاثة، فإن منها:
١٨ - المثلث المتساوي الاضلاع ، وهو، الذي اضلاعه الثلاث، مساوٍ، بعضها لبعض.
١٩ - المثلث المتساوي الساقيين، وهو، الذي ضلعين من اضلاعه فقط، متساويان.
٢٠ - المثلث المختلف الاضلاع، وهو، الذي اضلاعه الثلاثة، غير متساوية، بعضها لبعض.

٢١ - المثلث القائم الزاوية، وهو، الذي له، زاوية قائمة.
٢٢ - المثلث المنفرج الزاوية، وهو، الذي له، زاوية منفرجة.
٢٣ - المثلث الحاد الزوايا، وهو، الذي كل واحد من زواياه الثلاثة، حادة.
اما الاشكال، ذوات الاضلاع الأربعة، فان منها:
٢٤ - المربع، وهو المتساوي الاضلاع، القائم الزوايا.
٢٥ - المختلف الطولين، وهو القائم الزوايا، وليس، بمتساوي الاضلاع.
٢٦ - المَعّين، وهو، المتساوي الاضلاع، وليس بقائم الزوايا.
٢٧ - الشبيه بالمعين، وهو، الذي، كل ضلعين، من اضلاعه متقابلان، متساويان، وكل زاويتين، من زواياه، متقابلتين، متساويتان، وليس، بمتساوي الأضلاع، ولا، قائم الزوايا.

٢٨ - وما كان، على غير ما وصفنا، من الاشكال، ذوات الاضلاع الأربعة، فليسمى، المنحرف.
المُصَادَرَات الخمس، وهي الأشياء، التي تحتاج، الى الاتفاق عليها.
١ - أن يؤتى، بخط مستقيم، من كل نقطة، الى كل نقطة.

٢ - أن تخرج، خط مستقيم، ذو نهاية، على استقامة، واتصال، إلى غير نهاية.

٣ - أن تخْطُنَ، دائرة، على كل نقطة، وتقرر، كل بعد.
٤ - أن كل الزوايا، القائمة، مساوية، بعضها لبعض.
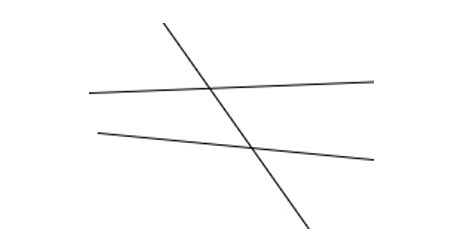
٥ - إن وقع، خط مستقيم، على، خطين مستقيمين، فصير، في إحدى الجهتين، الزاويتين الداخليتين، أصغر، من قائمتين، فإن الخطين المستقيمين، إذا خرجا، في تلك الجهة، إلتقيا.
علم عام، متفق عليه، أي، علوم متعارفة
١ - الأشياء المساوية، لشيء واحد، بعينه، هي متساوية.
٢ - إن زيد، على المتساوية، متساوية، صارت كلها، متساوية.
٣ - إن زيد، على غير المتساوية، متساوية، صارت كلها، غير، متساوية.
٤ - إن نقص، من المتساوية، متساوية، صارت الباقية، متساوية.
٥ - إن نقص، من غير المتساوية، متساوية، صارت الباقية، غير متساوية.
٦ - التي كل واحد منها، مثلان، لواحد بعينه، فهي، متساوية.
٧ - التي كل واحد منها، نصف، المقدار بعينه، فهي أيضا، متساوية.
٨ - التي لا يفضل، أحدهما على الاخر، إذا انطبق، بعضها على بعض، فهي، متساوية.
٩ - الكل أعظم، من الجزء.
١٠ - الكل مساو، لجميع اجزائه.
١١ - خطان مستقيمان، لا يحيطان، بسطح.
١ - أن نقيم، مثلثا، متساوي الاضلاع، على خط مستقيم، ذي نهاية، مفروض.
ليكن، الخط المستقيم، ذو النهاية، المفروض، خط أ ب.
ينبغي:
ان نقيم، على خط، أ ب المستقيم، مثلثا، متساوي الاضلاع.
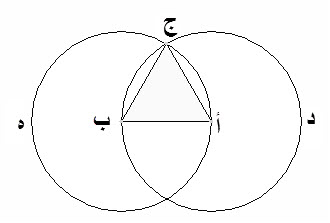
نخط، على مركز أ، وببعد أ ب، دائرة، وهي، ج د ب.
نخط أيضا، على مركز ب، وببعد ب أ، دائرة، وهي ج أ ه.
نصل، نقطة ج، التي تتقاطع عليها، الدائرتان، بنقطتي، أ ب، بخطين مستقيمين، وهما، ج أ، ج ب.
أقول:
إني قد اقمت، على خط أ ب، المفروض، مثلثا، متساوي الاضلاع، وهو مثلث، ج أ ب.
برهان ذلك:
نقطة أ، مركز دائرة، ج د ب.
خط، ج أ، مساو، لخط، أ ب.
نقطة ب، مركز دائرة ج أ ه.
خط، ج ب، مساو، لخط أ ب.
خطوط، ج أ، ج ب، أ ب، الثلاثة، متساوية لشيء واحد بعينه، فهي متساوية.
خط، ج أ، مساو، لخط، ج ب.
أقمنا، على خط، أ ب، المستقيم، ذو النهاية، المفروض، مثلثا، متساوي الاضلاع.
ذلك، ما أردنا، أن نبين.
٢ - أن نضيف، الى نقطة مفروضة، خطا، مستقيما، مساو، لخط، مستقيم، مفروض.
فليكن، النقطة المفروضة، أ، والخط المستقيم، المفروض، خط ب ج.
ينبغي:
أن نضيف، إلى نقطة، أ المفروضة، خطاً، مستقيما، مساويا، لخط، ب ج، المستقيم، المفروض.
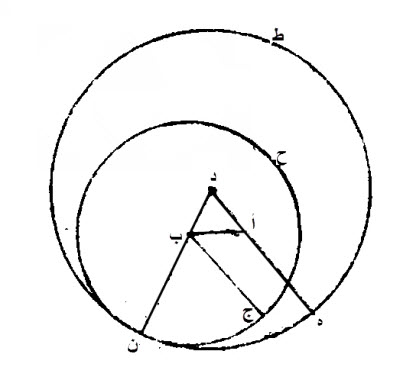
نصل، بين نقطة أ، ونقطة ب، خطا مستقيما، وهو خط، أ ب.
نقيم، على أ ب، مثلثا، متساوي الاضلاع، وهو، د أ ب.
نخرج، خطي، أ ه، ب ن، المستقيمين، على استقامة خطي، د أ، د ب المستقيمين.
نخط على ب، وببعد ب ج، دائرة، ح ج ن.
نخط على د، وببعد د ن، دائرة ط ه ن.
نقطة د، مركز، دائرة، ط ه ن.
خط، د ه، مساو، لخط، د ن.
مثلث، د أ ب، متساوي الاضلاع.
خط، د أ، مساو، لخط، د ب.
خط، أ ه، الباقي، مساو، لخط ب ن، الباقي.
نقطة ب، مركز، دائرة، ح ج ن.
خط، ب ج، مساو، لخط، ب ن.
خط أ ه، مساو، لخط، ب ج.
اضفنا، الى نقطة، أ المفروضة، خطا مستقيما، مساو، لخط، ب ج، المستقيم، وهو، أ ه.
ذلك، ما أردنا، أن نبين.
٣ - أن نفصل، من الأعظم، من، خطين، مستقيمين، مفروضين، غير متساويين، خطا، مساويا، لأصغرهما.
ليكن، الخطان، المستقيمان، المفروضان، اللذان، ليسا بمتساويين، خطا، أ ب، ج.
أعظمهما، أ ب.
ينبغي:
أن نفصل، من خط، أ ب، خطا مستقيما، مساويا، لخط، ج.
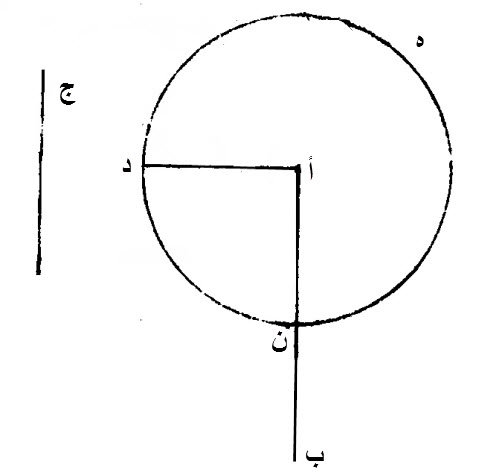
نصل، بنقطة أ، خطا مستقيما، مساويا، لخط، ج، وهو، أ د.
نخط، على مركز أ، وببعد، أ د، دائرة، ه د ن.
نقطة أ، مركز دائرة، ه د ن.
خط أ د ، مساو، لخط، أ ن.
خط أ د، مساو، لخط، ج.
خط أ ن، مساو، لخط، ج.
فصلنا من الأعظم، من، خطي، أ ب، ج، المستقيمين، المفروضين، الذين ليس بمتساويين، وهو أ ب، خطا، مساويا، لأصغرهما، وهو، ج، يكون، أ ن.
ذلك، ما أردنا، أن نبين.
٤ - إذا ساوى، ضلعان، من مثلث، ضلعين، من مثلث آخر، كل ضلع لنظيره، وتساوت، الزاوية، من كل منهما، التي تحيط بها، الخطوط، المستقيمة، المتساوية، من كل منهما فإن:
- القاعدة، مساوية للقاعدة.
- المثلث، مساو، للمثلث.
- سائر الزوايا، مساوية، لسائر الزوايا، كل واحدة، لنظيرتها، التي يوترها الضلع، المساوي، للضلع، التي يوترها، الاولى.
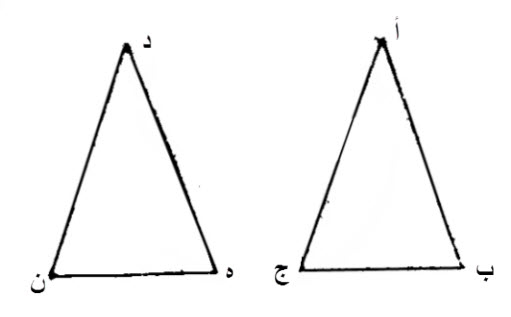
ليكن مثلثان، عليهما، أ ب ج، د ه ن.
ليكن، ضلعا، أ ب، أ ج، من أحدهما، مساويين، لضلعي، د ه، د ن، من الآخر، كل واحد لنظيره، اما ضلع أ ب، فلضلع، د ه، وأما ضلع، أ ج، فلضلع، د ن.
ليكن، الزاوية، التي يحيط بها، أ ب، أ ج، مساوية، للزاوية، التي يحيط بها، د ه، د ن.
أقول:
إن قاعدة، ب ج، أيضا مساوية، لقاعدة، ه ن، وإن مثلث، أ ب ج، مساو، لمثلث، د ه ن، وإن سائر الزوايا، مساوية، لسائر الزوايا، كل واحدة لنظيرتها، التي يوترها الضلع، المساوي، للضلع الذي يوتر، الأولى، فأما زاوية، أ ب ج، فلزاوية د ه ن، وأما زاوية، أ ج ب، فلزاوية، د ن ه.
برهان ذلك:
إذا ركب، مثلث، أ ب ج، على مثلث، د ه ن:
- وضع أ ب، على ضلع، د ه.
- وقعت نقطة، أ، على نقطة، د.
- تركب، ضلع، أ ج، على ضلع، د ن، لأن زاوية، ب أ ج، مساوية، لزاوية ه د ن.
- وقعت، نقطة، ب، على نقطة، ه.
- وقعت، نقطة، ج، على نقطة، ن.
- إنطبقت، قاعدة، ب ج، على قاعدة، ه ن، وصارت، مساوية لها.
- إنطبق، مثلث، أ ب ج، على مثلث، د ه ن، وصار، مساويا له.
- إنطبقت، سائر الزوايا، على سائر الزوايا، وصار بعضها، مساو، لبعض، كل واحدة، للتي يوترها الضلع، المساوي، للضلع، الذي يوتر الأخرى. فأما زاوية، أ ب ج، فلزاوية د ه ن، وأما زاوية، أ ج ب، فلزاوية، د ن ه.
فإذا ساوى، ضلعان، من مثلث، ضلعين، من مثلث آخر، كل ضلع لنظيره، وتساوت، الزاويتان منهما، اللتان، تحيط بهما، الخطوط، المستقيمة، المتساوية، فإن، القاعدة، مساوية للقاعدة، والمثلث، مساو، للمثلث، وسائر الزوايا، مساوية، لسائر الزوايا، كل واحدة، لنظيرتها، التي يوترها الضلع، المساوي، للضلع، التي يوترها، الاولى.
ذلك، ما أردنا، أن نبين.
٥ - الزاويتان، اللتان، عند القاعدة، من المثلثات، المتساوية الساقين، متساويتان، وإن أخرجت، الخطوط المستقيمة المتساوية، فان الزاويتين، التين، تحت القاعدة، تكونا متساويتين.
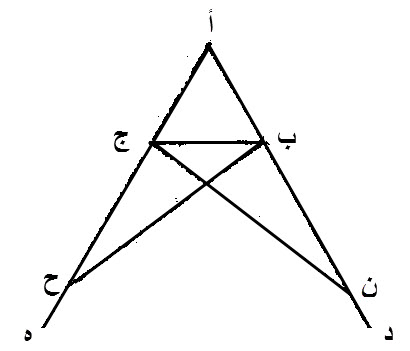
فليكن، مثلث، متساوي الساقين، أ ب ج، وليكن، ضلع، أ ب، مساو، لضلع، أ ج.
ليخرج، خطي، ب د، ج ه، المستقيمين، على استقامة خطي، أ ب، أ ج، المستقيمين.
أقول:
إن زاوية، أ ب ج، مساوية، لزاوية، أ ج ب، وأن زاوية، ج ب د مساوية، لزاوية، ب ج ه.
برهان ذلك:
نعلم، على خط، ب د، نقطة، كيف ما وقعت، وهي، ن.
نفصل، من خط، أ ه، خطا مساويا، لخط، أ ن، وهو، أ ح.
نصل، خطي، ج ن، ب ح.
خط، أ ن، مساو، لخط، أ ح.
خط، أ ج، مساو، لخط أ ب.
هذه الأضلاع، تحيط، بزاوية واحدة مشتركة، وهي زاوية، ب أ ج.
قاعدة ب ح، مساوية، لقاعدة ج ن.
مثلث، أ ج ن، مساو، لمثلث أ ب ح.
سائر الزوايا، مساوية، لسائر الزوايا، كل واحدة، لنظيرتها، التي يوترها، الضلع المساوي، للضلع، الذي يوتر الأولى.
زاوية، أ ج ن مساوية، لزاوية، أ ب ح.
زاوية، أ ن ج، مساوية، لزاوية، أ ح ب.
خط أ ن، مساو، لخط، أ ح.
خطا أ ب، أ ج، منهما متساويان.
خط، ب ن، الباقي، مساو، لخط، ج ح، الباقي.
كِلا خطي، ب ن، ج ن، مساويان، لكِلا خطي، ج ح، ب ح، كل واحد لنظيره، وزاوية، ب ن ج، مساوية، لزاوية، ج ح ب.
مثلث، ب ج ن، مساو، لمثلث ب ج ح.
سائر الزوايا منه، مساوية، لسائر الزوايا، كل واحدة لنظيرتها، التي يوترها الضلع، الذي، يوتر الأولى.
زاوية ب ج ح، مساوية لزاوية ج ب ن، وهما اللتان تحت القاعدة.
زاوية، ب ج ن، مساوية لزاوية، ج ب ح.
جميع زاوية، أ ج ن، مساوية، لجميع زاوية، أ ب ح.
زاوية أ ج ب الباقية، مساوية لزاوية أ ب ج، الباقية، وهما الزاويتان، اللتان عند القاعدة.
فالزاويتان، اللتان، عند القاعدة، من المثلثات، المتساوية الساقين، متساويتان، وإن أخرجت، الخطوط المستقيمة المتساوية، فان الزاويتين، التين، تحت القاعدة، تكونا متساويتين.
ذلك، ما أردنا، أن نبين.
٦ - إذا تساوت، زاويتان، من مثلث، فإن الضلعين، الذين، يوترانهما، يكونان، متساويان.
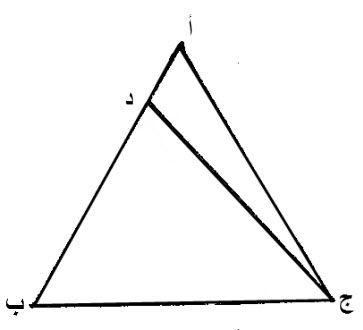
فليكن، زاوية، أ ج ب، من مثلث، أ ج ب، مساوية، لزاوية، أ ب ج، منه.
أقول:
إن ضلع، أ ج، مساو، لضلع، أ ب
برهان ذلك:
إن لم يكن، ضلع، أ ج، مساو، لضلع، أ ب، فإن أحدهما، أعظم، من الآخر.
ليكن الأعظم، أ ب، إن أمكن ذلك.
نفصل، من أ ب، الأعظم، خطا مساويا، لخط، أ ج، الأصغر، وهو د ب.
نصل، د ج.
خط أ ج، مساو، لخط د ب.
خط ج ب مشترك.
يكون، كِلا خطي، أ ج، ج ب، مساويان، لكِلا خطي، د ب، ج ب، كل واحد لنظيره.
زاوية، أ ج ب، مساوية، لزاوية، د ب ج.
قاعدة، أ ب، مساوية، لقاعدة، د ج.
مثلث أ ج ب، مساو لمثلث د ج ب.
الأصغر للأعظم، هذا خلف، لا يمكن.
ليس أ ب، أعظم، من أ ج.
كذلك نبين، أنه ليس، بأصغر منه.
خط أ ب مساو لخط أ ج.
فإذا تساوت، زاويتان، من مثلث، فإن الضلعين، الذين، يوترانهما، يكونان، متساويان.
ذلك، ما أردنا، أن نبين.
٧ - ليس يقوم، على خط، واحد، مستقيم، خطان مستقيمان، مساويين، لخطين آخرين مستقيمين، كل واحد لنظيره، يكون، ملتقاهما، وملتقى الاخرين، في جهة واحدة، على نقطتين مختلفتين، وبدايتهما، بداية الخطين، المساويين، لهما.
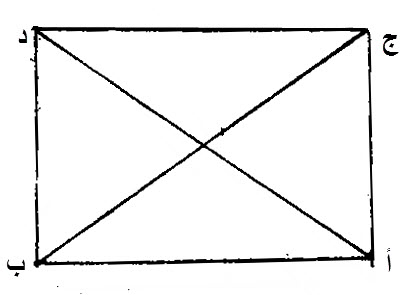
إن أمكن، فليقم، على خط، أ ب، المستقيم، خطا، ج أ، ج ب، المستقيمان.
ليقم، خطان آخران، مساويان لهما، كل واحد، لنظيره، وهما، د أ، د ب.
ليكن، ملتقاهما، وملتقى الآخرين، في جهة واحدة، على نقطيين مختلفتين، هما، ج و د.
لتكن، بدايتهما، بدايتا، الخطيين، المساويين لهما، فأما بدايتا، خطي، ج أ، د أ، فنقطة أ، وأما بدايتا، خطي، ج ب، د ب، فنقطة ب.
نصل، خط، ج د.
خط ج أ، مساو، لخط، د أ.
زاوية، د ج أ، مساوية، لزاوية، ج د أ.
زاوية، ج د أ، أعظم، من زاوية، د ج ب.
زاوية، ج د ب، أعظم كثيرا، من زاوية، د ج ب.
ج ب، مساو لخط د ب.
زاوية د ج ب، مساوية لزاوية ج د ب.
قد كان تبين، أنها أعظم منها، وهذا غير ممكن.
فليس يقوم، على خط، واحد، مستقيم، خطان مستقيمان، مساويين، لخطين آخرين مستقيمين، كل واحد لنظيره، يكون، ملتقاهما، وملتقى الاخرين، في جهة واحدة، على نقطتين مختلفتين، وبدايتهما، بداية الخطين، المساويين، لهما.
ذلك، ما أردنا، أن نبين.
٨ - إذا ساوى، ضلعان، من مثلث، ضلعين، من مثلث آخر، كل واحد لنظيره، وتساوت، قاعدتهما، فإن الزاويتين، اللتين تحيط بهما، الاضلاع المتساوية، متساويتان.
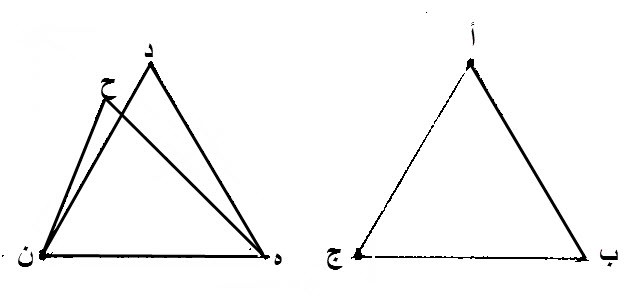
ليكن مثلثان، عليهما، أ ب ج، د ه ن.
ليكن، ضلعا أ ب، أ ج، من أحدهما، مساويان، لضلعي، د ه، د ن، من الآخر، كل واحد لنظيره، اما ضلع أ ب، فلضلع د ه، وأما ضلع أ ج، فلضلع د ن.
ليكن، قاعدة ب ج، مساوية، لقاعدة، ه ن.
أقول:
إن زاوية، ب أ ج، مساوية، لزاوية، ه د ن.
برهان ذلك:
إذا ركب، مثلث، أ ب ج، على مثلث د ه ن:
- وقعت قاعدة، ب ج، على، قاعدة، ه ن.
- وقعت، نقطة ب، على نقطة، ه.
- وقعت، نقطة، ج، على نقطة، ن.
وقع ضلعا، أ ب، أ ج، على ضلعي، د ه، د ن.
إن وقعت، قاعدة، ب ج، على قاعدة ه ن، ولم يقع، ضلعا، أ ب، أ ج، على ضلعي، د ه، د ن، ووقعا، على غير نقطة د، كخطي، ح ه، ح ن، فقد قام على خط واحد مستقيم، خطان مستقيمان، مساويين لخطين آخرين مستقيمين، كل واحد لنظيره، وصار ملتقاهما، وملتقى الآخرين، من جهة واحدة، على نقطتين مختلفتين، وبدايتهما، بدايتا، الخطين، المساويين لهما، وليس ذلك بممكن.
فإذا ركب مثلث أ ب ج، على مثلث د ه ن، ووضعت قاعدة ب ج، على قاعدة ه ن، ووقع ضلعا أ ب، أ ج، على ضلعي، د ه، د ن، ووقعت نقطة أ، على نقطة د، صارت، زاوية، ب أ ج، مساوية، ه د ن.
فإذا ساوى، ضلعان من مثلث، ضلعين، من مثلث آخر، كل واحد لنظيره، وتساوت، قاعدتهما، فإن الزاويتين، اللتين تحيط بهما، الاضلاع المتساوية، متساويتان.
ذلك، ما أردنا، أن نبين.
٩ - أن نقسم، زاوية مفروضة، مستقيمة الخطين، نصفين.
ليكن، الزاوية المفروضة، المستقيمة الخطين، زاوية، ب أ ج.
ينبغي:
أن نقسمها، بنصفين.
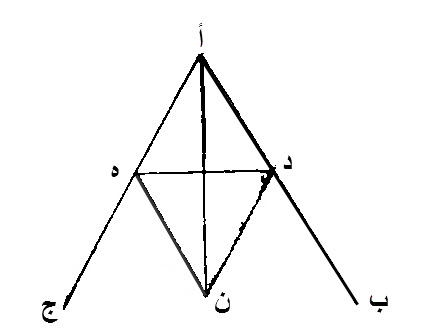
نعلم، على خط، أ ب، نقطة، كيفما وقعت، وهي، د.
نفصل، من خط، أ ج، خط، أ ه، مساويا لخط، أ د.
نصل، خط د ه، ونقيم، على خط، د ه، المستقيم، مثلثا، متساوي الاضلاع، وهو، د ه ن.
نصل خط، أ ن.
خط أ د، مساويا، لخط، أ ه.
خط، أ ن، مشترك.
كِلَيّْ خطي، أ د، أ ن، مساويين، لكِلَيّْ خطي، أ ه، أ ن، كل واحد لنظيره، وقاعدة، د ن، مساوية، لقاعدة، ه ن.
زاوية، د أ ن، مساوية، لزاوية، ه أ ن.
قد قسمت، زاوية، ب أ ج، المفروضة، المستقيمة الخطين، لنصفين، بخط، أ ن، المستقيم.
ذلك، ما أردنا، أن نبين.
١٠ - أن نقسم، خطا، مستقيما، مفروضا، ذو نهاية، نصفين.
ليكن، الخط، المستقيم، المفروض، ذو النهاية، أ ب.
ينبغي:
أن نقسمه، بنصفين.
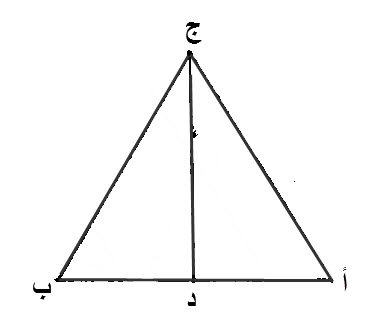
نقيم، على خط، أ ب، مثلثا، متساوي الاضلاع، وهو، ج أ ب.
نقسم، زاوية، أ ج ب، بنصفين، بخط، ج د المستقيم.
خط، ج أ، مساو، لخط، ج ب.
خط، ج د، مشترك.
كِلَيّْ خطي، ج أ، ج د، مساويين، لكلي خطي، ج ب، ج د، كل واحد لنظيره، وزاوية، أ ج د، مساوية، لزاوية، د ج ب.
قاعدة، أ د، مساوية، لقاعدة، د ب.
قسم، خط، أ ب، المستقيم، المفروض، ذو النهاية، بنصفين، على نقطة د.
ذلك، ما أردنا، أن نبين.
١١ - أن نخرج، من نقطة مفروضة، على خط مستقيم، مفروض، خطا مستقيما، على زاوية، قائمة.
ليكن، الخط، المفروض، أ ب.
لتكن، النقطة، المفروضة، التي عليه، نقطة ج.
ينبغي:
أن نخرج، من نقطة ج، خطا مستقيما، يكون، على زوايا قائمة، من خط، أ ب.
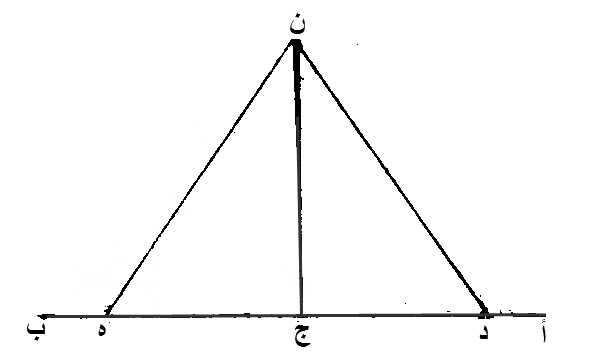
نعلم، على، خط أ ج، نقطة، كيف ما وقعت، وهي، د.
نفصل، من خط ج ب، خطا مساويا، لخط، د ج، وهو، ج ه.
نفرض، على د ه، مثلثا، متساوي الاضلاع، وهو، ن د ه.
نصل، خط، ن ج.
خط د ج، مساو، لخط، ج ه.
خط، ن ج، مشترك.
كِلَيّْ خطي،ن ج، د ج، مساويين، لكلي خطي، ن ج، ج ه، كل واحد لنظيره، وقاعدة، ن د، مساوية، لقاعدة، ن ه، لان المثلث، ن د ه، متساوي الاضلاع.
زاوية، ن ج د، مساوية، لزاوية، ن ج ه، وهما اللتان، على الجنبين.
إذا قام خط مستقيم، فصير، الزاويتين، التين على جنبيه، متساويتين، فكل واحدة منهما، قائمة.
كل واحدة، من زاويتي، ن ج د، ن ج ه، قائمة.
خط، ن ج، قائم، على خط، أ ب، على زوايا، قائمة.
أخرج، من نقطة ج، من خط، أ ب، خطا، على زوايا قائمة، وهو، ن ج.
ذلك، ما أردنا، أن نبين.
١٢ - أن نخرج، الى خط، مستقيم، مفروض، غير متناهي، من نقطة مفروضة، ليست عليه، خطا مستقيما، يكون، عمودا، على الخط.
ليكن، الخط، المستقيم، المفروض، الذي ليس بمتناهي، أ ب.
لتكن، النقطة، المفروضة، التي ليست عليه، نقطة ج.
ينبغي:
أن نخرج، من نقطة ج، الى خط، أ ب، المستقيم، خطا، يكون، عمودا عليه.
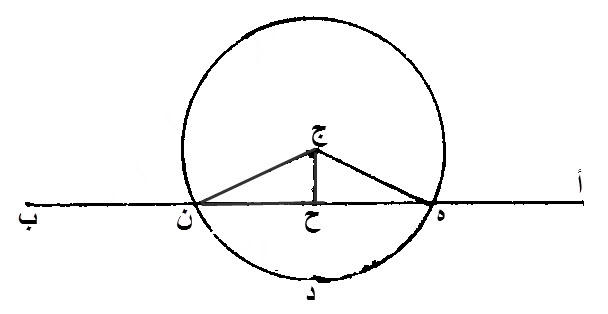
نعلم، من الجهة الأخرى، من الخط المستقيم، نقطة، كيف ما وقعت، وهي د.
نخط، على مركز ج، وببعد، ج د، دائرة، ه ن د.
نقسم، خط ه ن، المستقيم، نصفين، على نقطة، ح.
نصل، خطوط، ج ه، ج ح، ج ن.
أقول:
إن ج ح، عمود، على أ ب.
برهان ذلك:
خط، ه ح، مساو، لخط، ح ن.
خط، ج ح مشترك.
كِلَيّْ خطي، ج ح، ه ح، مساويين، لكلي خطي، ج ح، ح ن، كل واحد لنظيره، وقاعدة، ج ه مساوية، لقاعدة، ج ن، لان نقطة ج، مركز، دائرة، ه ن د.
زاوية، ه ج ح، مساوية، لزاوية، ح ج ن، وهما، اللتان، عن الجنبين.
إذا قام، خط مستقيم، على خط مستقيم، فصير، الزاويتين، التين عن جنبيه، متساويتين، فإن كل واحدة منهما قائمة، والخط، يقال له، العمود، على الخط، الذي هو قائم عليه.
خط، ج ح، عمود، على خط، أ ب.
قد خرج، الى خط، أ ب، المستقيم، المفروض، الذي ليس بمتناهي، من نقطة ج، المفروضة، التي ليست عليه، خط، مستقيم، عامود عليه، وهو، ج ح.
ذلك، ما أردنا، أن نبين.
١٣ - إذا قام، خط مستقيم، على خط مستقيم، كيف ما وقع، فإنه يحدث، زاويتين قائمتين، أو مساويتين، لقائمتين.
ليقم، خط، أ ب، المستقيم، على خط، ج د، المستقيم، وليحدث، زاويتي، ج ب أ، أ ب د.
أقول:
إن زاويتي، ج ب أ، أ ب د، إما قائمتين، إما، مساويتين، لقائمتين.
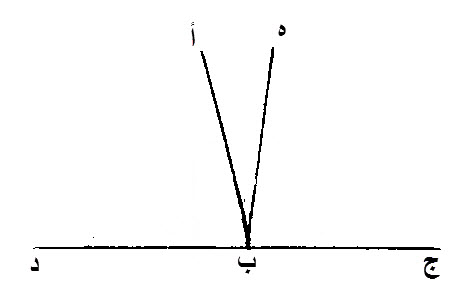
برهان ذلك:
إن كان، أ ب، قائما، على ج د، على زاوية قائمة، فإن زاويتي، ج ب أ، أ ب د، قائمتين.
إن لم يكن، أ ب، قائما، على ج د، على زوايا قائمة، فليخرج، من نقطة ب، من خط، ج د، خط، ه ب، على زوايا قائمة.
زاويتا، ج ب ه، ه ب د، قائمتان.
زوايا، ج ب ه، ه ب أ، أ ب د، الثلاث، مساوية، لزاويتي، ج ب ه، ه ب د، القائمتين، فزاويتا، ج ب أ، أ ب د، مساويتان، لقائمتين.
فإذا قام، خط مستقيم، على خط مستقيم، كيف ما وقع، فإنه يحدث، زاويتين قائمتين، أو إما، متساويتين، لقائمتين.
ذلك، ما أردنا، أن نبين.
١٤ - إذا أضيف، الى نقطة، على خط مستقيم، خطان مستقيمان، ليسا في جهة واحدة، فصيرا، الزاويتين، اللتين عن الجنبين، مساويتين لقائمتين، فإن كل، واحد من الخطين المستقيمين، على استقامة الآخر.
ليضف، الى نقطة ب، التي، على خط، أ ب المستقيم، خطا، ج ب، ب د، المستقيمين، اللذين ليسا بموضوعين، في جهة واحدة، وليصيرا، زاويتي، أ ب ج، أ ب د، اللتين، على الجنبين، مساويتين لقائمتين.
أقول:
إن ج ب، على إستقامة، ب د، ولا يمكن، إلا ذلك.
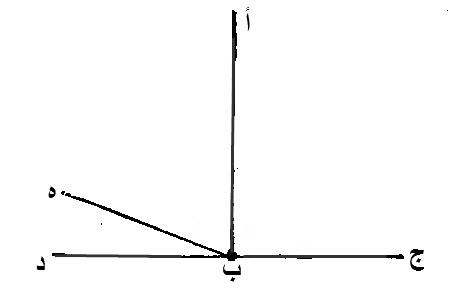
برهان ذلك:
إن أمكن، غير ذلك، فليكن، ه ب، على استقامة، ج ب.
خط أ ب، المستقيم، قد قام، على خط، ج ب ه، وأحدث زاويتي، أ ب ج، أ ب ه.
يكون، زاويتا، أ ب ج، أ ب ه، متساويتين، لقائمتين.
زاويتا، أ ب ج، أ ب د، قد وضعتا، انهما متساويتان، لقائمتين.
زاويتا، أ ب ج، أ ب د، مساويتين، لزاويتي، أ ب ج، أ ب ه.
نلقي، زاوية، أ ب ج، المشتركة.
يبقى، زاوية، أ ب د، الباقية، مساوية، لزاوية، أ ب ه، الباقية.
العظمى، مثل الصغرى، وهذا غير ممكن.
فليس، ب ه، على استقامة، ب ج.
كذلك نبين، أنه ليس خط آخر، على استقامة ب ج، غير ب د.
خط ب د، على استقامة، خط، ب ج.
فإذا أضيف، الى نقطة، على خط مستقيم، خطان مستقيمان، ليسا في جهة واحدة، فصيرا، الزاويتين، اللتين عن الجنبين، مساويتين لقائمتين، فإن كل، واحد من الخطين المستقيمين، على استقامة الآخر.
ذلك، ما أردنا، أن نبين.
١٥ - إذا قطع، كل واحد، من خطين، مستقيمين، الآخر، فإنهما، يُصَيِران، كل زاويتين، تتقابلان من الزوايا، التي تحدث، متساويتين.
ليقطع، كل واحد، من خطي، أ ب، د ج، المستقيمين، الآخر، على نقطة ه.
أقول:
إن زاوية، أ ه د، مساوية، لزاوية، ج ه ب، وإن زاوية، أ ه ج، مساوية، لزاوية، د ه ب.
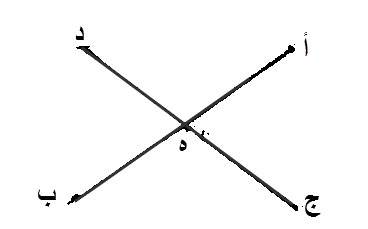
برهان ذلك:
قام، خط ما مستقيم، وهو ج ه، على خط، أ ب، المستقيم، وأحدث زاويتين، أ ه ج، ج ه ب.
زاويتا، أ ه ج، ج ه ب، مساويتين، لقائمتين.
خط، أ ه، المستقيم، قد قام، على خط، د ج، المستقيم، وأحدث زاويتين، أ ه د، أ ه ج.
زاويتا، أ ه د، أ ه ج، مساويتين، لقائمتين.
زاويتي، أ ه د، أ ه ج، مساويتان لزاويتي، أ ه ج، ج ه ب.
يلقى، زاوية، أ ه ج المشتركة، فزاوية أ ه د الباقية، مساوية لزاوية، ج ه ب الباقية، وهما المتقابلتان.
كذلك أيضا، نبين، أن زاوية، أ ه ج، مساوية، لزاوية، د ه ب.
فإذا قطع، كل واحد، من خطين، مستقيمين، الآخر، فإنهما، يُصَيِران، كل زاويتين، تتقابلان من الزوايا، التي تحدث، متساويتين.
ذلك، ما أردنا، أن نبين.
كذلك، قد تبين من هذا، انه، إذا قطع، كل واحد، من خطين مستقيمين، الآخر، فانهما، يصيران الزوايا، التي عند تقاطعهما، مساوية، لأربع زوايا، قائمة.
١٦ - كل مثلث، يخرج، ضلع من أضلاعه، فإن الزاوية، الخارجة، أعظم، من كل واحدة، من الزاويتين، الداخليتين، المقابلتين لها.
فليكن مثلث، عليه، أ ب ج.
ليخرج، ضلع، ب ج، من أضلاعه، على استقامته، الى نقطة، د.
أقول:
إن زاوية، أ ج د، الخارجة، من مثلث، أ ب ج، أعظم، من كل واحد، من زاويتي، ب أ ج، أ ب ج، الداخليتين، المقابلتين لها.
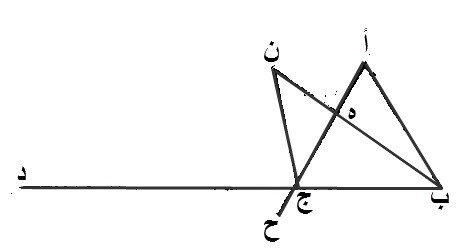
برهان ذلك:
نقسم، أ ج، بنصفين، على نقطة، ه.
نصل ه ب.
نخرج، خط ه ن المستقيم، على إستقامة، خط، ب ه.
نجعل، خط ن ه، مساويا، لخط ه ب.
نصل، ن ج.
نخرج، خط، ج ح، المستقيم، على إستقامة، خط، أ ج.
خط أ ه، مساو، لخط، ه ج.
خطه ب، مساو، لخط، ن ه.
كلي خطي، أ ه، ه ب، مساويين، لكلي خطي، ه ج، ن ه، كل واحد لنظيره، وزاوية، أ ه ب، مساوية، لزاوية، ن ه ج ، لانهما متقابلتان.
قاعدة أ ب، مساوية، لقاعدة، ن ج.
مثلث أ ه ب، مساو، لمثلث، ن ه ج.
سائر الزوايا، مساوية، لسائر الزوايا، كل واحدة لنظيرتها، التي يوترها الضلع، المساوي، للضلع، الذي يوتر، الأخرى.
زاوية، ه أ ب، مساوية لزاوية ن ج ه.
زاوية، ه ج د، أعظم، من زاوية، ن ج ه.
زاوية أ ج د، أعظم، من زاوية، ب أ ج.
كذلك أيضا، نبين، من قسمة، خط، ب ج، بنصفين، أن زاوية، ب ج ح، مساوية، لزاوية، أ ج د، لانهما متقابلتان، فزاوية، أ ج د، أعظم، من زاوية، أ ب ج.
فكل مثلث، يخرج، ضلع من أضلاعه، فإن الزاوية، الخارجة، أعظم، من كل واحدة، من الزاويتين، الداخليتين، المقابلتين لها.
ذلك، ما أردنا، أن نبين.
١٧ - كل زاويتين، من مثلث، أي زاويتين، كانتا، فهما، أصغر، من قائمتين.
فليكن مثلث، عليه، أ ب ج.
أقول:
إن كل زاويتين، من زوايا، مثلث، أ ب ج، أي زاويتين، كانتا، أصغر، من قائمتين.
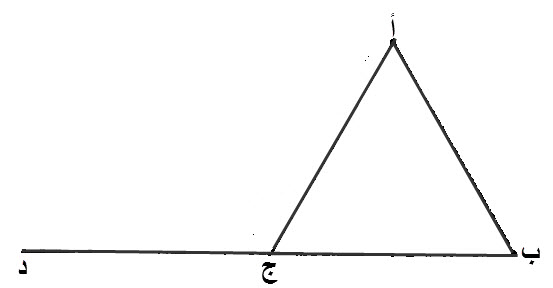
برهان ذلك:
نخرج، خط، ج د، المستقيم، على استقامة خط، ب ج.
زاوية، أ ج د، الخارجة، من مثلث، أ ب ج، تكون، أعظم، من الزاوية، التي تقابلها، الداخلة، وهي زاوية، أ ب ج.
ليكن، زاوية، أ ج ب، مشتركة.
زاويتي، أ ج ب، أ ج د، أعظم، من زاويتي، أ ج ب، أ ب ج.
زاويتا أ ج ب، أ ج د، مساويتين، لقائمتين.
زاويتا، أ ب ج، أ ج ب، أصغر من قائمتين.
كذلك، نبين، أن زاويتا، ج أ ب، ج ب أ، أصغر، من قائمتين، وأن زاويتي، ب أ ج، ب ج أ، أيضا، أصغر من قائمتين.
فكل زاويتين، من مثلث، أي زاويتين، كانتا، فهما، أصغر، من قائمتين.
ذلك، ما أردنا، أن نبين.
١٨ - الضلع الأعظم، من كل مثلث، يوتر، الزاوية العظمى.
ليكن مثلث، عليه، ج أ ب.
ليكن، ضلع، أ ب منه، أعظم، من ضلع، ج أ.
أقول:
إن زاوية، أ ج ب، أعظم، من زاوية، ج ب أ.
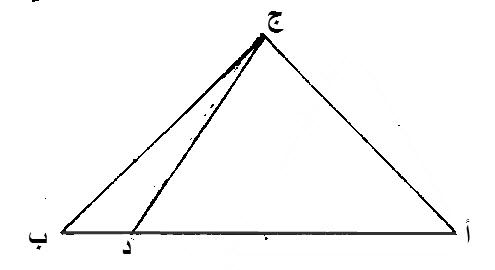
برهان ذلك:
ضلع أ ب، أعظم، من ضلع، ج أ.
نجعل أ د، مثل ج أ، ونصل، ج د.
خط ج أ، مساو، لخط أ د.
زاوية، أ ج د، مساوية، لزاوية، ج د أ.
زاوية، أ ج ب، أعظم، من زاوية، أ ج د.
زاوية، أ ج ب، أعظم، من زاوية، ج د أ.
زاوية، ج د أ، خارجة، عن مثلث، ج د ب.
ج د أ، أعظم، من الزاوية الداخلة، التي تقابلها، التي عليها، ج ب أ.
زاوية أ ج ب، قد تبين، إنها أعظم، من زاوية، ج د أ.
زاوية، أ ج ب، أعظم كثيرا، من زاوية، ج ب أ.
فالضلع الأعظم، من كل مثلث، يوتر، الزاوية العظمى.
ذلك، ما أردنا، أن نبين.
١٩ - الزاوية العظمى، من كل مثلث، يوترها، الضلع الأعظم.
ليكن، مثلث، عليه، أ ب ج.
ليكن، زاوية، أ ج ب، منه، أعظم، من زاوية، أ ب ج.
أقول:
إن ضلع، أ ب، أعظم، من ضلع، أ ج.
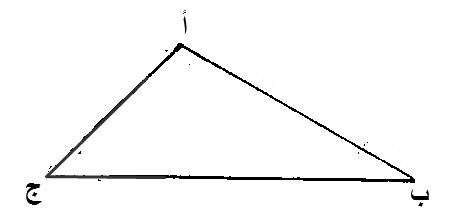
برهان ذلك:
إن لم يكن، ضلع، أ ب، أعظم، من ضلع، أ ج، فهو، مساو له، أو، أصغر منه.
ليس ضلع، أ ب، مساو، لضلع، أ ج، لأنه، لو كان مساوٍ له، لكانت، زاوية، أ ج ب، مساوية، لزاوية، أ ب ج، وليست كذلك، فليس، ضلع، أ ب، بمساو، لضلع، أ ج.
وليس ضلع، أ ب، بأصغر، من ضلع، أ ج، لأنه، لو كان ضلع، أ ب، أصغر، من ضلع، أ ج، لكانت، زاوية، أ ج ب، أصغر، من زاوية، أ ب ج، وليست كذلك، فليس ضلع، أ ب، بأصغر، من ضلع، أ ج.
قد كان تبين، أن ضلع، أ ب، ليس بمساو، لضلع، أ ج، فضلع أ ب، أعظم، من ضلع، أ ج.
فالزاوية العظمى، من كل مثلث، يوترها، الضلع الأعظم.
ذلك، ما أردنا، أن نبين.
٢٠ - كل ضلعين، من مثلث، أي ضلعين، كانا، أعظم، من الضلع، الباقي.
ليكن مثلث، عليه، أ ب ج.
أقول:
إن كل ضلعين، من المثلث، أي ضلعين، كانا، أعظم، من الضلع الباقي.
أما، أ ب، أ ج، فأعظم، من، ب ج، وأما، أ ب، ب ج، فأعظم، من، أ ج، وأما، أ ج، ب ج، فأعظم، من، أ ب.
برهان ذلك:
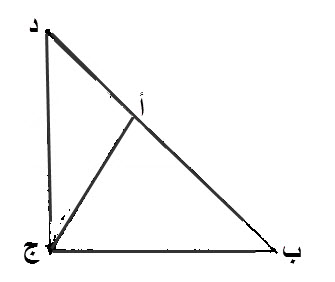
ليخرج، خط، أ د المستقيم، على استقامة، خط ب أ.
نجعل، خط د أ، مساويا، لخط، أ ج.
نصل، خط، د ج.
خط، د أ، مساو لخط أ ج، يكون، زاوية د ج أ، مساوية، لزاوية، أ د ج.
زاوية، د ج ب، أعظم، من زاوية، د ج أ.
زاوية، د ج ب، أعظم، من زاوية، ب د ج.
الزاوية العظمى، من كل مثلث، يوترها، الضلع الأعظم.
ضلع، د ب، أعظم، من ضلع، ب ج.
ضلع، د ب، مساو، لضلعي، أ ب، أ ج.
ضلعا، أ ب، أ ج، أعظم، من ضلع، ب ج.
كذلك نبين، أن ضلعي، أ ب، ب ج، أعظم، من ضلع، أ ج.
فكل ضلعين، من مثلث، أي ضلعين، كانا، أعظم، من الضلع، الباقي.
ذلك، ما أردنا، أن نبين.
٢١ - إذا قام على ضلع، من أضلاع مثلث، خطان مستقيمان، يخرجان من طرفي الضلع، وكانا في داخل المثلث، فإنهما، أصغر من الضلعيين الباقيين، من أضلاع المثلث، ويحيطان، بزاوية أعظم، من الزاوية، التي يحيط بها، الضلعان الباقيان.
ليكن مثلث، عليه، أ ب ج.
ليقم، على ضلع، ب ج، من أضلاع مثلث، أ ب ج، خطان مستقيمان، يخرجان من طرفيه، ويقعان، في داخل المثلث، عليهما، د.
أقول:
إن خطي، د ب، د ج، أصغر، من خطي أ ب، أ ج، وأن زاوية، ب د ج، التي يحيطان بها، أعظم، من زاوية، ب أ ج.
برهان ذلك:
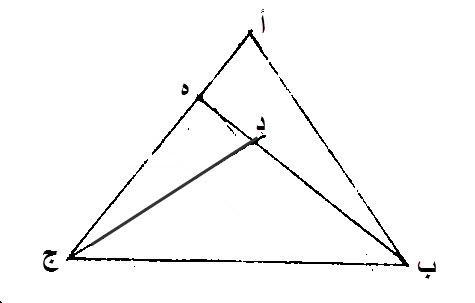
نخرج، خط، د ه، المستقيم، على استقامة، خط، ب د.
كل ضلعين، من مثلث، أي ضلعين، كانا، هما، أعظم، من الضلع الثالث.
خطا، أ ه، أ ب، أعظم، من خط، ه ب.
نجعل، ه ج مشتركا.
خطا، أ ج، أ ب، أعظم، من خطي، ه ب، ه ج.
كل ضلعين، من مثلث، أي ضلعين، كانا، هما، أعظم، من الضلع الباقية.
خطا، ه د، ه ج، أعظم، من خط، د ج
نجعل، خط، د ب، مشتركا.
خطا، ه ب، ه ج، أعظم، من خطي، د ب، د ج
قد تبين، أن خطي، أ ب، أ ج، أعظم، من خطي، ه ب، ه ج.
خطا، أ ب، أ ج، أعظم كثيرا، من خطي، د ب، د ج.
زاوية، ب د ج، الخارجة، عن مثلث، ه د ج، تكون، أعظم، من زاوية، د ه ج، الداخلة، التي تقابلها.
زاوية، د ه ج، أيضا، خارجة عن مثلث، أ ه ب، تكون، أعظم، من زاوية، ب أ ه، الداخلة، التي تقابلها.
قد تبين، أن زاوية، ب د ج، أعظم، من زاوية، د ه ج.
زاوية، ب د ج، أعظم كثيرا، من زاوية، ب أ ج.
فإذا قام على ضلع، من أضلاع مثلث، خطان مستقيمان، يخرجان من طرفي الضلع، وكانا في داخل المثلث، فإنهما، أصغر من الضلعيين الباقيين، من أضلاع المثلث، ويحيطان، بزاوية أعظم، من الزاوية، التي يحيط بها، الضلعان الباقيان.
ذلك، ما أردنا، أن نبين.
٢٢ - أن نقيم، مثلثا، من ثلاثة خطوط، مستقيمة، مساوية، لثلاثة خطوط، مستقيمة، مفروضة، وينبغي، أن يكون، كل خطين، من الخطوط الثلاثة، أي خطين كانا، أعظم، من الخط الباقي.
ليكن، الثلاثة الخطوط، المستقيمة، المفروضة، أ، ب، ج.
ليكن، كل خطين منها، أي خطين كانا، أعظم، من الخط الباقي.
أ، ب، أعظم من ج.
ب، ج، أعظم من أ.
أ، ج، أعظم من، ب.
ينبغي:
أن نقيم مثلثا، تساوي اضلاعه، خطوط، أ، ب، ج.
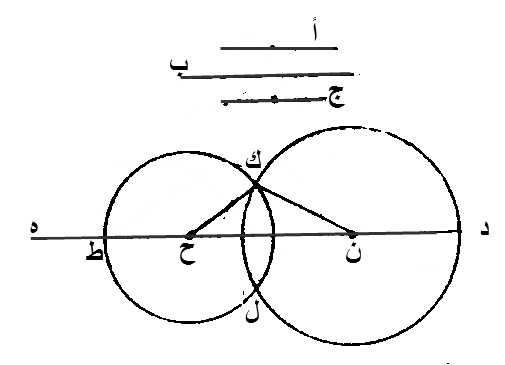
نجعل، خط د ه، المستقيم، منهيا، من إحدى الجهتين، الى نقطة، د، وغير منتهيا، في الجهة التي فيها، ه.
نجعل، خط د ن، مساويا، لخط، أ؛ خط ن ح، مساويا، لخط، ب؛ خط ح ط، مساويا، لخط، ج.
نخط، على مركز ن، وببعد د، دائرة، ك د ل.
نخط، على مركز ح، وببعد، ط، دائرة، ك ط ل.
نخرج، من نقطة ك، الى نقطتي، ن، ح، خطي، ك ن، ك ح، المستقيمين.
أقول:
إن مثلث، ك ن ح، قد أقيم، من ثلاثة خطوط، مستقيمة، مساوية لخطوط، أ، ب، ج، المستقيمة.
برهان ذلك:
نقطة ن، مركز دائرة، ك د ل.
يكون، خط، ك ن، مساو، لخط، د ن.
خط،أ ، مساو، لخط، د ن.
خط، أ، مساو، لخط، ك ن.
نقطة ح، مركز دائرة، ك ط ل.
خط، ك ح، مساو، لخط، ح ط.
خط، ج، مساو، لخط، ح ط.
خط، ج، مساو، لخط، ك ح.
خط، ب، مساو، لخط، ن ح.
قد أقيم، من خطوط، ك ن، ك ح، ن ح، المستقيمة، المساوية، لخطوط، أ، ج، ب، المستقيمة، المفروضة، مثلث، ك ن ح.
ذلك، ما أردنا، أن نبين.
٢٣ - أن نقيم، على خط، مستقيم، مفروض، على نقطة منه، مفروضة، زاوية، مستقيمة الخطين، مساوية، لزاوية مفروضة، مستقيمة الخطين.
ليكن، الخط المستقيم المفروض، أ ب.
لتكن، النقطة المفروضة، التي عليه، أ.
لتكن، الزاوية المفروضة، المستقيمة، الخطين، د ج ه.
ينبغي:
أن نقيم على خط، أ ب، المستقيم، المفروض، على نقطة، أ منه، زاوية، مستقيمة الخطين، مساوية، لزاوية، د ج ه، المفروضة، المستقيمة الخطين.
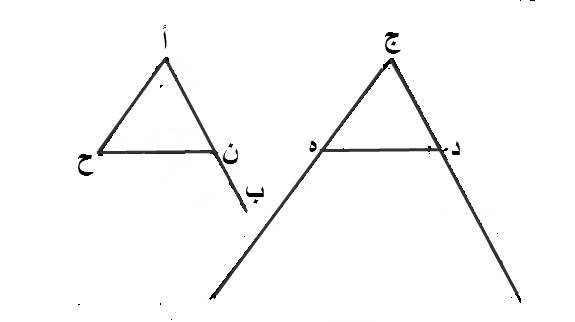
نعلم، على كل واحد، من خطي، ج د، ج ه، نقطة، كيف ما وقعت، د، ه.
نصل، د ه.
نقيم، مثلثا، من خطوط، أ ن، أ ح، ن ح، الثلاثة، المستقيمة، المساوية لخطوط، ج د، ج ه، د ه، المستقيمة المفروضة، وهو مثلث، أ ن ح.
ليكن، خط، أ ن، منه، مساويا، لخط، ج د، وخط، أ ح، لخط، ج ه، وخط، ن ح، لخط، د ه.
خطي، ج د، ج ه، مساويان، لخطي، أ ن، أ ح، كل واحد لنظيره.
قاعدة، د ه، مساوية، لقاعدة، ن ح.
يكون، زاوية د ج ه، مساوية، لزاوية، ب أ ح.
قد قام، على خط أ ب، المستقيم، المفروض، على نقطة، أ منه، زاوية، مستقيمة الخطين، مساوية، لزاوية، د ج ه، المفروضة، المستقيمة الخطين، وهي، زاوية، ن أ ح.
ذلك، ما أردنا، أن نبين.
٢٤ - إذا كان مثلثان، وكان ضلعان، من أحدهما، مساويين، لضلعين، من الآخر، كل واحد لنظيره، والزاوية، التي تحيط بها الضلعين، من أحدهما، أعظم، من الزاوية، التي تحيط بها، الضلعان المساويان لهما، من المثلث الاخر، فإن قاعدة، المثلث، العظيم الزاوية، أعظم، من قاعدة، المثلث الآخر.
ليكن مثلثان، عليهما، أ ب ج، د ه ن.
ليكن، ضلعا، أ ب، أ ج، مساويين، لضلعي، د ه، د ن، كل واحد لنظيره، اما ضلع، أ ب، فلضلع، د ه، واما ضلع، أ ج، فلضلع، د ن.
لتكن، زاوية، ب أ ج، أعظم، من زاوية، ه د ن.
أقول:
إن قاعدة، ب ج، أعظم، من قاعدة، ه ن.
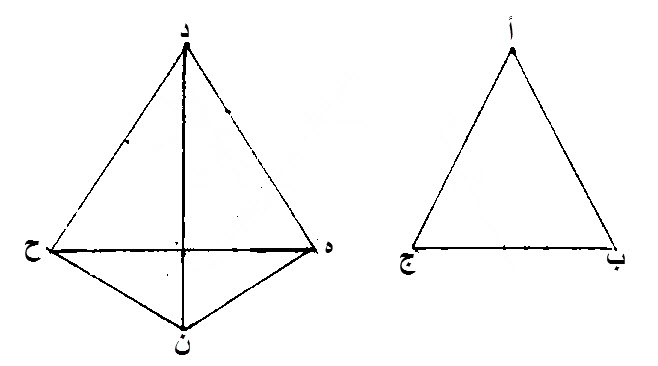
برهان ذلك:
زاوية، ب أ ج، أعظم، من زاوية، ه د ن.
نقيم، على خط، د ه، المستقيم، على نقطة، د منه، زاوية، مستقيمة الخطين، مساوية، لزاوية، ب أ ج، المستقيمة، وهي زاوية، ه د ح، المستقيمة الخطين.
نجعل، خط، د ح المستقيم، مساويا، لكل واحد، من خطي، أ ج، د ن.
نصل خطي، ه ح، ح ن.
خط أ ب، مساو، لخط، د ه
خط أ ج، مساو، لخط، د ح.
كلي خطي، أ ب، أ ج، مساويين، لكلي خطي، د ه، د ح، كل واحد لنظيره، وزاوية، ب أ ج، مساوية، لزاوية، ه د ح.
قاعدة ب ج، مساوية، لقاعدة، ه ح.
خط، د ح، مساو، لخط، د ن.
زاوية د ن ح، مساوية، لزاوية، د ح ن.
زاوية، د ن ح، أعظم، من زاوية، ه ح ن.
زاوية، ه ن ح، أعظم كثيرا، من زاوية، ه ح ن
الزاوية العظمى، من كل مثلث، يوترها، الضلع الأعظم.
ضلع، ه ح، أعظم، من قاعدة، ه ن.
ضلع ه ح، مساو، لضلع ب ج، فقاعدة، ب ج، أعظم، من قاعدة، ه ن.
فإذا كان مثلثان، وكان ضلعان، من أحدهما، مساويين، لضلعين، من الآخر، كل واحد لنظيره، والزاوية، التي تحيط بها الضلعين، من أحدهما، أعظم، من الزاوية، التي تحيط بها، الضلعان المساويان لهما، من المثلث الاخر، فإن قاعدة، المثلث، العظيم الزاوية، أعظم، من قاعدة، المثلث الآخر.
ذلك، ما أردنا، أن نبين.
٢٥ - إذا كان مثلثان، وضلعان، من أحدهما، مساويين، لضلعين، من الآخر، كل واحد لنظيره، وكانت، القاعدة، أعظم، من القاعدة، فإن الزاوية، التي تحيط بها الضلعان، من المثلث العظيم القاعدة، أعظم، من الزاوية، التي تحيط بها الضلعان، المساويان لهما، من المثلث الآخر.
ليكن، مثلثان، عليهما، أ ب ج، د ه ن.
ليكن، ضلعا، أ ب، أ ج، من أحدهما، مساويين، لضلعي، د ه، د ن، من الآخر، كل واحد لنظيره اما ضلع، أ ب، فلضلع، د ه، وأما ضلع، أ ج، فلضلع، د ن.
لتكن، قاعدة، ب ج، أعظم، من قاعدة، ه ن.
أقول:
إن زاوية، ب أ ج، أعظم، من زاوية، ه د ن.
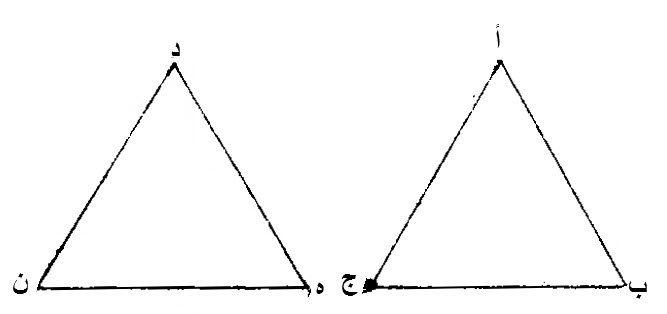
برهان ذلك:
إن لم يكن كذلك، فهي، إما، مساوية لها، إما، أصغر منها.
ليست، زاوية ب أ ج، بمساوية، لزاوية، ه د ن. لأنها، لو كانت مساوية لها، لكانت، قاعدة، ب ج، مساوية، لقاعدة، ه ن، وليست، كذلك، فليست زاوية، ب أ ج، مساوية، لزاوية ه د ن.
ولا هي، بأصغر منها، لأنها، لو كانت أصغر منها، لكانت، قاعدة، ب ج، أصغر، من قاعدة، ه ن، وليست كذلك، فليست زاوية، ب أ ج، أصغر، من زاوية، ه د ن.
قد كان تبين، انها ليست، بمساوية لها، فزاوية ب أ ج، أعظم، من زاوية، ه د ن.
فإذا كان مثلثان، وضلعان، من أحدهما، مساويين، لضلعين، من الآخر، كل واحد لنظيره، وكانت، القاعدة، أعظم، من القاعدة، فإن الزاوية، التي تحيط بها الضلعان، من المثلث العظيم القاعدة، أعظم، من الزاوية، التي تحيط بها الضلعان، المساويان لهما، من المثلث الآخر.
ذلك، ما أردنا، أن نبين.
٢٦ - إذا كان مثلثان، وكانت، زاويتان، من أحدهما، مساويتين، لزاويتين، من الآخر، كل واحدة لنظيرتها، وكان ضلع، من أحدهما، مساو، لضلع، من الآخر، إما الضلع، الذي يلي الزاويتين، لنظيره، وإما، الذي يوتر، إحدى الزاويتين، للذي يوتر، الزاوية، المساوية لها، فإن الضلعيين الباقيين، مساويين، للضلعين الباقيين، كل واحد لنظيره، والزاوية الباقية، مساوية، للزاوية الباقية.
ليكن، مثلثان، عليهما، د ه ن، أ ب ج.
ليكن، زاويتا، د ه ن، د ن ه، من أحدهما، مساويتين، لزاويتي، أ ب ج، أ ج ب، من الآخر، كل واحد لنظيرتها، اما زاوية، د ه ن، فلزاوية، أ ب ج، وأما زاوية، د ن ه، فلزاوية، أ ج ب.
ليكن، ضلع من أحدهما، مساو، لضلع من الآخر.
ليكن أولا:
الضلعان، المتساويان منهما، الضلعان، اللذان يليان، الزوايا، المتساوية، وهما، ه ن، ب ج.
أقول:
إن الاضلاع الباقية، مساوية، للأضلاع الباقية، كل واحد لنظيره، أما ضلع، د ه، فلضلع، أ ب، وأما ضلع، د ن، فلضلع، أ ج، وإن، زاوية، ه د ن، الباقية، مساوية، لزاوية، ب أ ج، الباقية
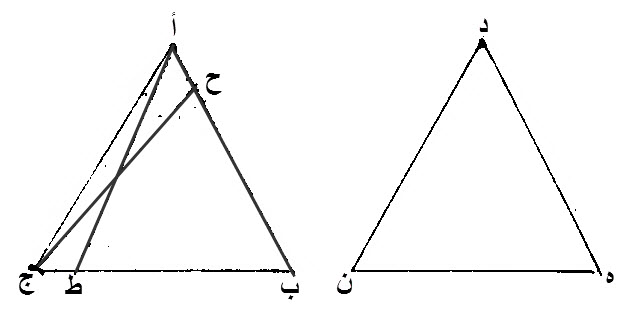
برهان ذلك:
إن لم يكن، ضلع د ه، مساويا، لضلع، أ ب، فإن أحدهما، أعظم، من الآخر.
ليكن الأعظم، أ ب، إن أمكن ذلك، ونفصل، من أ ب، خطا مساويا، لخط، د ه، وهو ح ب.
نصل، ح ج.
خط، د ه، مساو، لخط، ح ب، وخط، ه ن، لخط ب ج.
يكون، كلي خطي، د ه، ه ن، مساويين، لكلي خطي، ح ب، ب ج، كل واحد لنظيره.
زاوية، د ه ن، مساوية، لزاوية، ح ب ج.
قاعدة، د ن، مساوية، لقاعدة، ح ج، ومثلث، د ه ن، مساو، لمثلث، ح ب ج، وسائر الزوايا، مساوية لسائر الزوايا، كل واحدة لنظيرتها، التي يوترها الضلع، المساوي للضلع، الذي يوتر الأولى.
زاوية، د ن ه، مساوية، لزاوية، ح ج ب.
زاوية، د ن ه، قد كانت مساوية، لزاوية، أ ج ب.
زاوية، أ ج ب، مساوية، لزاوية، ح ج ب.
العظمى، للصغرى، هذا خلف، لا يمكن.
فليس خط، أ ب، غير مساو، ل، د ه، فهو، مساو له.
خط ه ن، مساو، لخط، ب ج.
كلي خطي، د ه، ه ن، مساويان، لكلي خطي، أ ب، ب ج، كل واحد لنظيره، وزاوية، د ه ن، مساوية، لزاوية، أ ب ج.
قاعدة، د ن، مساوية، لقاعدة، أ ج، ومثلث، د ه ن، مساو، لمثلث، أ ب ج، وسائر الزوايا، مساوية، لسائر الزوايا، التي يوترها، الاضلاع المتساوية.
زاوية، ه د ن، مساوية، لزاوية، ب أ ج.
ليكن أيضا:
الضلعان، المتساويان، من أضلاع مثلثي، د ه ن، أ ب ج، ضلعان، يوتران، زاويتين متساويتين، وهما، د ه، أ ب.
أقول:
إن سائر الاضلاع، مساوية، لسائر الاضلاع، كل واحد لنظيره، أما ضلع، د ن، فلضلع، أ ج، وأما ضلع، ه ن، فلضلع، ب ج، وأن زاوية، ه د ن، الباقية، مساوية، لزاوية، ب أ ج، الباقية.
إن لم يكن، ضلع، ه ن، مساويا، لضلع، ب ج، فإن أحدهما، أعظم من الآخر، فليكن الأعظم، ب ج.
نفصل، من خط، ب ج، خطا، مساويا، لخط، ه ن، وهو ب ط.
نصل، أ ط.
خط، د ه، مساو، لخط، أ ب، وخط، ه ن، لخط، ب ط.
كلي، من خطي، د ه، ه ن، مساويين، لكلي خطي، أ ب، ب ط، كل واحد لنظيره.
زاوية، د ه ن، مساوية، لزاوية، أ ب ط.
قاعدة، د ن، مساوية، لقاعدة، أ ط، ومثلث، د ه ن، مساو، لمثلث، أ ب ط، وسائر الزوايا، مساوية، لسائر الزوايا، التي توترها، الاضلاع المتساوية.
زاوية، د ن ه، مساوية، لزاوية، أ ط ب .
زاوية، د ن ه، مساوية، لزاوية، أ ج ب.
زاوية، أ ط ب، مساوية، لزاوية، أ ج ب.
الخارجة للداخلة، ذلك غير ممكن.
ليس، خط، ب ج، غير مساو، لخط، ه ن، فهو إذا، مساو له.
خط د ه، مساو، لخط، أ ب.
كلي خطي، د ه، ه ن، مساويان، لكلي خطي، أ ب، ب ج، كل واحد لنظيره.
زاوية، د ه ن، مساوية، لزاوية، أ ب ج.
قاعدة، د ن، مساوية، لقاعدة، أ ج، ومثلث، د ه ن، مساو، لمثلث، أ ب ج، وسائر الزوايا، مساوية، لسائر الزوايا، التي يوترها، الاضلاع المتساوية.
زاوية، ه د ن، مساوية، لزاوية، ب أ ج.
فإذا كان مثلثان، وكانت، زاويتان، من أحدهما، مساويتين، لزاويتين، من الآخر، كل واحدة لنظيرتها، وكان ضلع، من أحدهما، مساو، لضلع، من الآخر، إما الضلع، الذي يلي الزاويتين، لنظيره، وإما، الذي يوتر، إحدى الزاويتين، للذي يوتر، الزاوية، المساوية لها، فإن الضلعيين الباقيين، مساويين، للضلعين الباقيين، كل واحد لنظيره، والزاوية الباقية، مساوية، للزاوية الباقية.
٢٧ - إذا وقع، خط ما، مستقيم، على خطين، مستقيمين، فصير الزاويتين، المتبادلتين، متساويتين، فإن كل واحد، من الخطين، المستقيمين، مواز للآخر.
ليقع، على، أ ب، ج د، المستقيمين، خطا، وهو، ه ن.
ليصير، الزاويتين، المتبادلتين، وهما، أ ه ن، ه ن د، متساويتين.
أقول:
إن خط، أ ب، مواز، لخط، ج د.
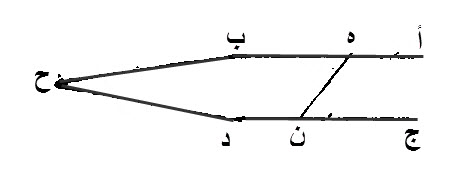
برهان ذلك:
إن لم يكن كذلك، فإن خطا، أ ب، ج د، إذا أخرجا، التقيا، إما من جهة، ب د، وإما، من جهة، أ ج.
فليلتقيا، من جهة، ب د، أولا، إن أمكن ذلك، في جهة ب د، على نقطة، ح.
زاوية، أ ه ن، خارجة، عن مثلث، ه ح ن، تكون، أعظم، من زاوية، ه ن د، الداخلة، التي تقابلها، ولكنها، مساوية لها، وهذا ما لا يمكن.
ليس يلتقي، خطا، أ ب، ج د، إذا أخرجا، في جهة، د ب.
كذلك أيضا، نبين، أنهما لا يلتقيان، في جهة، أ ج.
الخطوط المستقيمة، التي لا تلتقي، في إحدى الجهتين، هي متوازنة.
خط أ ب، مواز، لخط، ج د.
فإذا وقع، خط ما، مستقيم، على خطين، مستقيمين، فصير الزاويتين، المتبادلتين، متساويتين، فإن كل واحد، من الخطين، المستقيمين، مواز للآخر.
ذلك، ما أردنا، أن نبين.
٢٨ - إذا وقع، خط مستقيم، على خطين مستقيمين، فصير، الزاوية الخارجة، مساوية للداخلة، التي تقابلها، أو صير، الزاويتين الداخلتين، التين، في جهة واحدة، مساويتين، لقائمتين، فإن كل واحد، من الخطين المستقيمين، مواز للآخر.
ليقع، على خطي، أ ب، ج د، المستقيمين، خط مستقيم، وهو خط، ه ن ح.
ليصير، زاوية، ه ن ب، الخارجة، مساوية، لزاوية، ن ح د، الداخلة، التي تقابلها، أو يصير، زاويتي، ب ن ح، ن ح د، الداخليتين، اللتين في جهة واحدة، وهي جهة، ب د، مساويتين، لقائمتين، فأقول:
إن خط، أ ب، مواز، لخط، ج د.
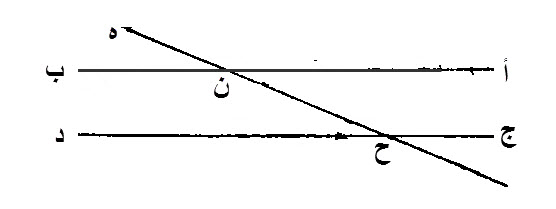
برهان ذلك:
زاوية ه ن ب، مساوية، لزاوية، أ ن ح، ولزاوية، ن ح د، يكون، زاوية، أ ن ح، مساوية، لزاوية، ن ح د، وهما المتبادلتان، فخط، أ ب، مواز، لخط، ج د.
ليكن أيضا، الزاويتان الداخليتان، اللتان في جهة واحدة، وهما، ب ن ح، ن ح د، مساويتين، لقائمتين، فأقول أيضا، إن خط، أ ب، مواز، لخط، ج د.
زاويتي، أ ن ح، ب ن ح، مساويتين، لقائمتين.
زاويتا، ب ن ح، ن ح د، هما مساويتان، لقائمتين.
زاويتا، أ ن ح، ب ن ح، مساويتين، لزاويتي، ب ن ح، ن ح د.
يلقى، زاوية، ب ن ح، المشتركة.
زاوية، أ ن ح، الباقية، مساوية، لزاوية، ن ح د، الباقية.
هما المتبادلتان.
خط، أ ب، مواز، لخط، ج د.
فإذا وقع، خط مستقيم، على خطين مستقيمين، فصير، الزاويتين، الخارجة مساوية للداخلة، التي تقابلها، أو صير، الزاويتين الداخلتين، التين، في جهة واحدة، مساويتين، لقائمتين، فإن كل واحد، من الخطين المستقيمين، مواز للآخر.
وذلك، ما أردنا، أن نبين.
٢٩ - إذا وقع، خط مستقيم، على خطين، مستقيمين، متوازيين، فإنه يصير، الزاويتين، المتبادلتين، متساويتين، ويصير، الزاوية الخارجة، مساوية، للزاوية الداخلة، التي تقابلها، ويصير، الزاويتين الداخليتين، اللتين، في جهة واحدة، مساويتين، لقائمتين.
ليقع، خط، ه ن ح، المستقيم، على خطي، أ ب، ج د، المستقيمين، المتوازيين.
أقول إنه:
- يصير، زاويتي، أ ن ح، ن ح د، المتبادلتين، متساويتين.
- يصير، زاوية، ه ن ب، مساوية، لزاوية، ن ح د.
- يصير، زاويتي، ب ن ح، ن ح د، الداخليتين، اللتين، في جهة واحدة، مساويتين، لقائمتين.
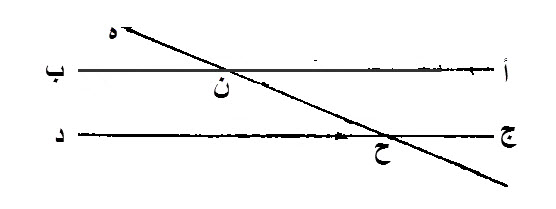
برهان ذلك:
إن كانت، زاوية، أ ن ح، غير مساوية، لزاوية، ن ح د، فإن إحداهما، أعظم، من الأخرى.
لتكن، زاوية، أ ن ح، أعظم.
أ ن ح، أعظم، إن أمكن ذلك.
نجعل، زاوية، ب ن ح، مشتركة.
زاويتا، أ ن ح، ب ن ح، أعظم، من زاويتي، ب ن ح، ن ح د.
زاويتي، أ ن ح، ب ن ح، مساويتين، لقائمتين.
زاويتا، ب ن ح، ن ح د، أصغر، من قائمتين.
الخطوط، المستقيمة، التي تخرج، من أقل، من زاويتين قائمتين، وتنفذ، الى ما لا نهاية، فإنها، تلتقي.
خطا، أ ب، ج د، إذا أخرجا، الى ما لا نهاية، التقيا.
هذان الخطان، لا يلتقيان، لأن، أ ب، يوازي، ج د.
ليست، زاوية، أ ن ح، غير مساوية، لزاوية، ن ح د، فهي إذا، مساوية لها، وهما، الزاويتان المتبادلتان.
زاوية، ه ن ب، مساوية، لزاوية، أ ن ح، لانهما، متقابلتان.
زاوية، ه ن ب، مساوية، لزاوية، ن ح د، وهي الخارجة، للداخلة، التي تقابلها.
نجعل، زاوية، ب ن ح، مشتركة.
زاويتا، ه ن ب، ب ن ح، مساويتين، لزاويتي، ب ن ح، ن ح د.
زاويتي، ه ن ب، ب ن ح، مساويتان، لقائمتين.
زاويتا، ب ن ح، ن ح د، مساويتان، لقائمتين.
فإذا وقع، خط مستقيم، على خطين، مستقيمين، متوازيين، فإنه يصير، الزاويتين، المتبادلتين، متساويتين، ويصير، الزاوية الخارجة، مساوية، للزاوية الداخلة، التي تقابلها، ويصير، الزاويتين الداخليتين، اللتين، في جهة واحدة، مساويتين، لقائمتين.
ذلك، ما أردنا، أن نبين.
٣٠ - إذا كانت خطوط، موازية، لخط واحد، بعينه، مستقيم، فإن بعضها، مواز، لبعض.
ليكن، كل واحد، من، أ ب، ج د، مواز، لخط، ه ن.
أقول:
إن أ ب، مواز، ل، ج د.
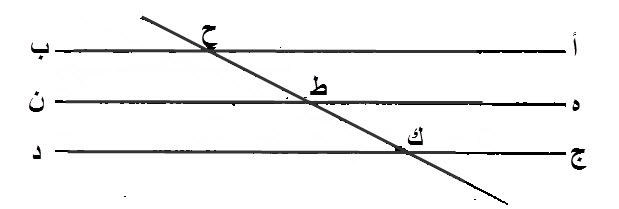
برهان ذلك:
ليقع، على الخطوط، خط ما، مستقيم، وهو خط، ح ط ك.
أ ب، مواز، ل، ه ن.
وقع عليهما، خط، ح ط، المستقيم، يكون، زاويتا، أ ح ط، ح ط ن، المتبادلتان، متساويتين.
ه ن، مواز، ل، ج د.
وقع عليهما، خط، ح ط ك، المستقيم، يكون، زاوية، ح ط ن، الخارجة، مساوية، ل، ط ك د، الداخلة، التي تقابلها.
زاوية، ح ط ن، أيضا مساوية، لزاوية، أ ح ط.
زاوية، أ ح ط، مساوية، لزاوية، ط ك د .
هما، متبادلتان.
أ ب، مواز، ل، ج د.
فإذا كانت خطوط، موازية، لخط واحد، بعينه، مستقيم، فإن بعضها، مواز، لبعض.
وذلك، ما أردنا، أن نبين.
٣١ - أن نخرج، من نقطة، مفروضة، خطا مستقيما، موازيا، لخط مستقيم، مفروض.
ليكن، النقطة المفروضة، نقطة أ.
ليكن، الخط المستقيم المفروض، خط، ج ب.
ينبغي:
أن نخرج، من نقطة، أ، خطا، مستقيما، موازيا، لخط، ج ب، المستقيم.
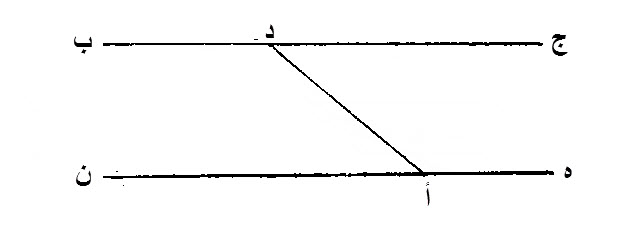
نعلم، على ج ب، نقطة، كيف ما وقعت، وهي، نقطة، د.
نصل، خط، د أ.
نقيم، على خط، د أ، المستقيم، على نقطة، أ منه، زاوية، مساوية، لزاوية، ب د أ، وهي زاوية، د أ ه.
نخرج، خط، أ ن، على استقامة، خط، ه أ.
خطي، ه ن، ج ب، المستقيمين، قد وقع عليهما، خط ما، مستقيم، وهو، د أ، فصير زاويتي، ب د أ، د أ ه، متساويتان، وهما، متبادلتان، يكون، ه ن، موازيا، ل، ج ب.
قد أخرج، من النقطة المفروضة، خطا، وهو، ه ن، موازيا، لخط، ج ب، المستقيم، المفروض.
ذلك، ما أردنا، أن نبين.
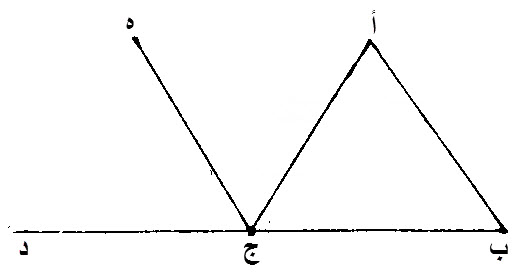
٣٢ - كل مثلث، يخرج، ضلع من أضلاعه، فإن، الزاوية الخارجة، تكون، مساوية، للزاويتين الداخلتين، التين، تقابلانها، والزوايا الثلاث، في داخل المثلث، مساوية، لزاويتين قائمتين.
ليكن، مثلث، عليه، أ ب ج.
ليخرج، أحد أضلاعه، وهو، ب ج، الى نقطة د.
أقول:
إن زاوية، أ ج د، الخارجة، مساوية، لزاويتي، أ ب ج، ب أ ج، الدخلتين، وإن، زوايا، ب أ ج، أ ب ج، أ ج ب، الثلاث، هي، من داخل المثلث، مساوية، لزاويتين قائمتين.
برهان ذلك:
نخرج، من نقطة، ج، خطا موازيا، لخط، أ ب، المستقيم، وهو، ه ج.
خط، أ ج، وقع، على خطين، متوازيين.
زاويتا، أ ج ه، ب أ ج، المتبادلتان، متساويتان.
أ ب، مواز، ل، ه ج، وقد وقع عليهما، خط، ب ج د، المستقيم.
زاوية، ه ج د، الخارجة، مساوية، لزاوية، أ ب ج، الداخلة، التي تقابلها.
زاوية، أ ج ه، أيضا، مساوية، لزاوية، ب أ ج.
جميع، زاوية، أ ج د، الخارجة، مساوية، لزاويتي، ب أ ج، ج ب أ، الداخلتين، اللتين، يقابلانها.
نجعل، زاوية، أ ج ب، مشتركة.
زاويتا، أ ج ب، أ ج د، مساويتان، لزوايا، ب أ ج، ج ب أ، أ ج ب.
زاويتي، أ ج ب، أ ج د، مساويتان، لزاويتين قائمتين.
زوايا، ب أ ج، ج ب أ، أ ج ب، مساوية، لقائمتين.
فكل مثلث، يخرج، ضلع من أضلاعه، فإن، الزاوية الخارجة، تكون، مساوية، للزاويتين الداخلتين، التين، تقابلانها، والزوايا الثلاث، في داخل المثلث، مساوية، لزاويتين قائمتين.
ذلك، ما أردنا، أن نبين.
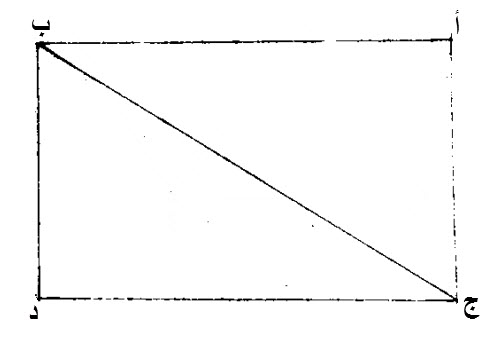
٣٣ - الخطوط المستقيمة، التي تصل، فيما بين، أطراف الخطوط، المستقيمة، المتوازية، المتساوية، في جهة واحدة، هي أيضا، متساوية، ومتوازية.
ليكن، خطان متوازيان، عليهما، أ ب، ج د.
ليصل، فيما بين طرفيهما، خطي، أ ج، ب د.
أقول:
إن، أ ج، ب د، أيضا، متساويان، متوازيان.
برهان ذلك:
نصل، ب ج.
أ ب، مواز، ل، ج د
قد وقع عليهما، خط مستقيم، وهو، ب ج.
زاويتا، أ ب ج، ب ج د، المتبادلتان، متساويتين.
أ ب، مساو، ل، ج د.
ب ج، مشترك.
كلي خطي، أ ب، ب ج، مساويين، لكلي خطي، ج د، ب ج، كل واحد لنظيره، وزاوية، أ ب ج، مساوية، لزاوية، ب ج د.
قاعدة، أ ج، مساوية، لقاعدة، ب د.
مثلث، أ ب ج، مساو، لمثلث، ب ج د.
سائر الزوايا، مساوية، لسائر الزوايا، كل واحدة لنظيرتها، التي يوترها، الضلع، المساوي، للضلع، الذي يوتر، الأخرى.
زاوية، أ ج ب، مساوية، لزاوية، ج ب د، وهما، متبادلتان.
أ ج، مواز، ل، ب د.
قد تبين، أنهما متساويان.
فالخطوط المستقيمة، التي تصل، فيما بين، أطراف الخطوط، المستقيمة، المتوازية، المتساوية، في جهة واحدة، هي أيضا، متساوية، ومتوازية.
ذلك، ما أردنا، أن نبين.
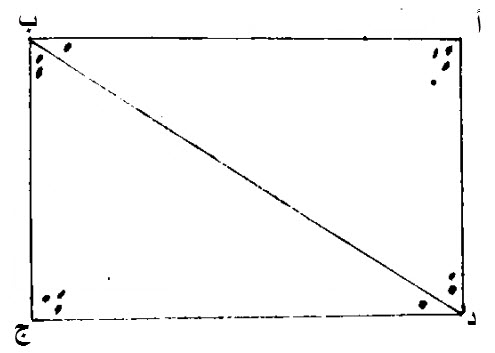
٣٤ - الاضلاع، والزوايا، المتقابلة، من السطوح، المتوازية الاضلاع، مساو، بعضها لبعض، وأقطار السطوح، تقسمها، بنصفين.
ليكن، سطح، أ ب ج د، متوازي الاضلاع.
ليكن، قطره، ب د .
أقول:
إن أضلاع، أ ب ج د، المتوازي الاضلاع، المتقابلة، وزواياه، المتقابلة، مساو، بعضها لبعض، وإن القطر، يقسمه، بنصفين.
برهان ذلك:
خط، أ د، مواز، لخط، ب ج.
وقع عليهما، خط، ب د.
زاويتا، أ د ب، د ب ج، المتبادلتان، متساويتين.
أ ب، مواز، ل، د ج.
وقع عليهما، خط، ب د، المستقيم.
زاويتا، أ ب د، ب د ج، المتبادلتان، متساويتان.
مثلثا، أ ب د، ب د ج:
- ساوت، زاويتا، أ ب د، أ د ب، من أحدهما، زاويتي، ب د ج، د ب ج، من الآخر، كل واحدة، لنظيرتها.
- في المثلثين، ضلع، مشترك لهما، يلي، الزوايا المتساوية، وهو، ب د.
سائر الأضلاع، مساوية، لسائر الاضلاع، كل واحد، لنظيره.
- خط، أ ب، لخط، د ج.
- خط، أ د، لخط، ب ج.
زاوية، د أ ب، الباقية، مساوية، لزاوية، د ج ب، الباقية.
مثلث، أ ب د، مساو، لمثلث، ب د ج.
زاوية، أ ب د، مساوية، لزاوية، ب د ج.
زاوية، د ب ج، مساوية، لزاوية، ب د أ.
زاوية، أ ب ج، كلها، مساوية، لزاوية، أ د ج.
قد تبين، أنَّ زاوية، د أ ب، مساوية، لزاوية، ب ج د.
فالأضلاع، والزوايا، المتقابلة، من السطوح، المتوازية الاضلاع، مساو، بعضها لبعض، وأقطار السطوح، تقسمها، بنصفين.
ذلك، ما أردنا، أن نبين.
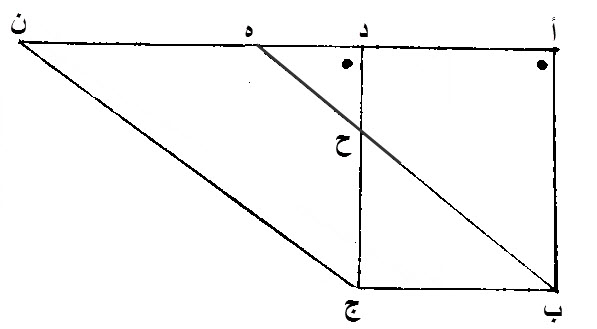
٣٥ - السطوح، المتوازية الاضلاع، التي، على قاعدة واحدة، وفي، جهة واحدة، وفيما بين خطوط بأعيانها متوازية، مساو، بعضها، لبعض.
ليكن، سطحان، متوازيا الاضلاع، عليهما، أ د ج ب، ه ن ج ب، على قاعدة واحدة، وهي، ب ج، وفيما بين، خطي، أ ن، ب ج، المتوازيين.
أقول:
إن سطح، أ د ج ب، المتوازي الاضلاع، مساو، لسطح، ه ن ج ب، المتوازي الاضلاع.
برهان ذلك:
أ د ج ب، سطح، متوازي الاضلاع، يكون، أ د، مساو، ل، ب ج.
ه ن ج ب، سطح، متوازي الاضلاع، يكون، ه ن، مساو، ل، ب ج.
أ د، مساو، ل، ه ن.
نجعل، د ه، مشتركا.
أ ه، كله، مساو، ل، د ن، كله.
أ ب، مساو، ل، د ج.
كلي خطي، أ ه، أ ب، مساويان، لكلي خطي، د ن، د ج، كل واحد لنظيره.
زاوية، ب أ ه مساوية، لزاوية، ج د ن، الخارجة، للداخلة.
قاعدة، ه ب، مساوية، لقاعدة، ن ج.
مثلث، أ ه ب، مساو، لمثلث، د ن ج.
نلقي، مثلث، د ه ح، المشترك.
يبقى، منحرف، أ د ح ب، مساو، لمنحرف، ه ن ج ح، الباقي.
نجعل، مثلث، ب ح ج، مشتركا.
جميع، سطح، أ د ج ب، المتوازي الأضلاع، مساو، لجميع سطح، ه ن ج ب، المتوازي، الاضلاع.
فالسطوح، المتوازية الاضلاع، التي، على قاعدة واحدة، وفي، جهة واحدة، وفيما بين خطوط بأعيانها متوازية، مساو، بعضها، لبعض.
ذلك، ما أردنا، أن نبين.
٣٦ - السطوح، المتوازية الاضلاع، التي، على قواعد، متساوية، وفى جهة واحدة، فيما بين خطوط، بأعينها متوازية، مساو، بعضها لبعض.
ليكن، سطحان، متوازيا الأضلاع، عليهما، أ ج د ب، ه ط ح ن، على قاعدتين، متساويتين، هما، ب د، ن ح، وفيما بين خطي، أ ط، ب ح، المتوازيين.
أقول:
إن سطح، أ ج د ب، المتوازي الاضلاع، مساو، لسطح، ه ط ح ن، المتوازي الاضلاع.
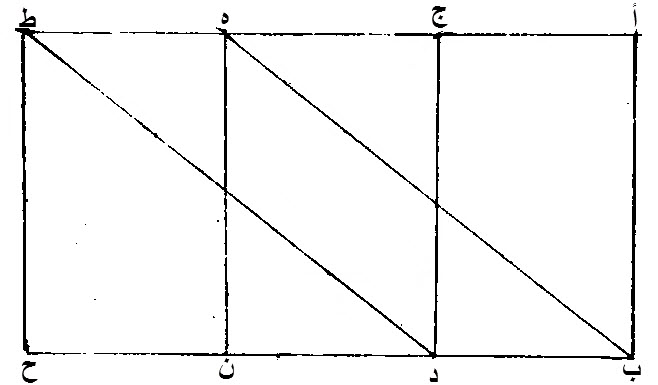
برهان ذلك:
نصل، خطي، ه ب، ط د.
ب د، مساو، ل، ن ح.
ه ط، مساو، ل، ن ح.
ه ط، مساو، ل، ب د.
هو أيضا، مواز، له.
الخطوط المستقيمة، التي تصل، فيما بين أطراف، الخطوط المستقيمة، المتوازية، التي، في جهة واحدة، هي أيضا، متساوية، متوازية.
خطا، ه ب، ط د، متساويان.
سطح، ه ط د ب، متوازي الاضلاع.
هو مساو، لسطح، أ ج د ب، المتوازي الاضلاع، لانهما، على قاعدة واحدة، وهي، ب د، وفيما بين خطين، متوازيين، بأعينهما، وهما، أ ط، ب ح.
كذلك، سطح، ه ط ح ن، المتوازي الاضلاع، مساو، لسطح، ه ط د ب المتوازي الاضلاع.
كل واحد، من سطحي، أ ج د ب، ه ط ح ن، مساو، لسطح، ه ط د ب.
المساوية، لواحد بعينه، هي متساوية.
سطح، أ ج د ب، المتوازي الاضلاع، مساو لسطح، ه ط ح ن، المتوازي الاضلاع.
فالسطوح، المتوازية الاضلاع، التي، على قواعد، متساوية، وفى جهة واحدة، فيما بين خطوط، بأعينها متوازية، مساو، بعضها لبعض.
ذلك، ما أردنا، أن نبين.
٣٧ - المثلثات، الّتي، على قاعدة واحدة، ومن جهة واحدة، وفيما بين خطوط، بأعينها متوازية، مساو، بعضها لبعض.
ليكن، مثلثا، أ ب ج، د ب ج، على قاعدة واحدة، وهي، ب ج، وفيما بين، خطي، أ د، ب ج، المتوازيين.
أقول:
إن مثلث، أ ب ج، مساو، لمثلث، د ب ج.
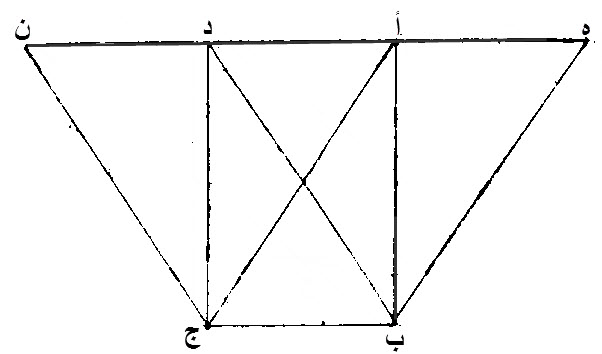
برهان ذلك:
نخرج، أ د، في الجهتين، الى نقطتي، ه، ن.
نخرج، من نقطة ب، خطا مستقيما، موازيا، لخط، أ ج، المستقيم، وهو، ه ب.
نخرج، من نقطة ج، خطا مستقيما، موازيا، لخط د ب، المستقيم، وهو، ن ج.
كل واحد، من سطحي، ه أ ج ب، د ن ج ب، متوازي الاضلاع.
سطح، ه أ ج ب، المتوازي الاضلاع، مساو، لسطح، د ن ج ب، المتوازي الاضلاع، لانهما، على قاعدة واحدة، وهي، ب ج، وفيما بين، خطي، أ د، ب ج، المتوازيين.
نصف سطح، ه أ ج ب، هو مثلث، أ ب ج، لأن، أ ب قطره، ونصف سطح، د ن ج ب، المتوازي الاضلاع، هو مثلث، د ب ج، لأن، د ج قطره.
الّتي هي، أنصاف الأشياء، أيضا متساوية.
فمثلث، أ ب ج، مساو، لمثلث، د ب ج.
فالمثلثات، الّتي، على قاعدة واحدة، ومن جهة واحدة، وفيما بين خطوط، بأعينها متوازية، مساو، بعضها لبعض.
ذلك، ما أردنا، أن نبين.
٣٨ - المثلثات، التي، على قواعد متساوية، وفي جهة واحدة، وفيما بين خطوط بأعينها متوازية، مساو، بعضها لبعض.
ليكن، مثلثا، أ ب ج، د ه ن، على قاعدتين، متساويتين، وهما، ب ج، ه ن، وفيما بين، خطي، أ د، ب ن، المتوازيين.
أقول:
إن مثلث، أ ب ج، مساو، لمثلث، د ه ن.
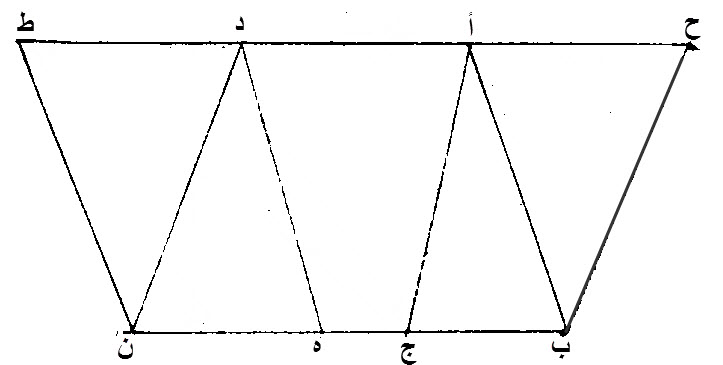
برهان ذلك:
نخرج، أ د، في الجهتين، الى نقطتي، ح، ط.
نخرج، من نقطة، ب، خطا مستقيما، موازيا، لخط، أ ج، المستقيم، وهو، ح ب.
نخرج، من نقطة ن، خطا، مستقيما، موازيا، لخط، د ه، المستقيم، وهو، ط ن.
كل واحد، من سطحي، ح أ ج ب، د ط ن ه، متوازي الاضلاع.
سطح، ح أ ج ب، المتوازي الاضلاع، مساو، لسطح، د ط ن ه، المتوازي الاضلاع، لأنهما، على قاعدتين، متساويتين، وهما، ب ج، ه ن وفيما بين، خطي، ح ط، ب ن، المتوازيين.
نصف سطح، ح أ ج ب، المتوازي الاضلاع، هو، مثلث، أ ب ج، لأن، أ ب قطره.
نصف سطح، د ط ن ه، المتوازي الاضلاع، هو، مثلث، د ه ن، لأن، د ن قطره.
التي هي، أنصاف، لأشياء، متساوية، هي أيضا، متساوية.
مثلث، أ ب ج، مساو، لمثلث، د ه ن.
فالمثلثات، التي، على قواعد متساوية، وفي جهة واحدة، وفيما بين خطوط بأعينها متوازية، مساو، بعضها لبعض.
ذلك، ما أردنا، أن نبين.
٣٩ - المثلثات المتساوية، التي، على، قاعدة واحدة، وفي، جهة واحدة، فهي، ما بين خطوط بأعيانها متوازية.
ليكن، مثلثا، أ ب ج، د ب ج، متساويين، وعلى، قاعدة واحدة، وهي، ب ج.
لنصل، خط، أ، د.
أقول:
إن، أ د، مواز، ل، ب ج.
برهان ذلك:
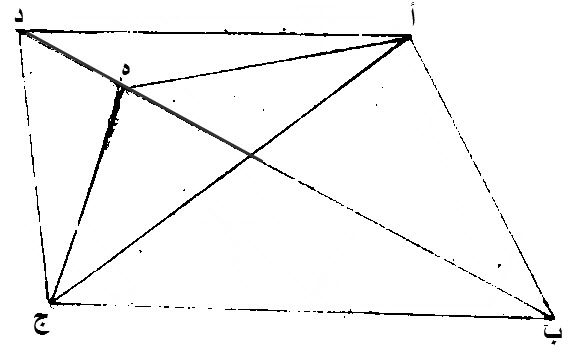
إن لم يكن، كذلك، فلنخرج، من نقطة، أ، خطا مستقيما، موازيا، لخط، ب ج، وهو، أ ه.
نصل، خط، ه ج.
مثلث، ه ب ج، مساو، لمثلث، أ ب ج، لأنهما، على قاعدة واحدة، وهي، ب ج، وفيما بين خطي، أ ه، ب ج، المتوازيين.
مثلث، أ ب ج، مساو، لمثلث، د ب ج.
مثلث، د ب ج، مساو، لمثلث، ه ب ج.
الأعظم، للأصغر، هذا غير ممكن.
ليس، خط أ ه، بمواز، لخط، ب ج.
كذلك أيضا، نبين، أنه لا يخرج، من نقطة أ، خط مواز، لخط، ب ج، غير، أ د.
فالمثلثات المتساوية، التي، على، قاعدة واحدة، وفي، جهة واحدة، فهي، ما بين خطوط بأعيانها متوازية.
ذلك، ما أردنا، أن نبين.
٤٠ - المثلثات، المتساوية، التي، على قواعد متساوية، وقواعدها، على خط مستقيم، وفي جهة واحدة، هي، فيما بين خطوط، بأعيانها، متوازية.
ليكن، مثلثا، أ ب ج، د ه ن، متساويين، وعلى، قاعدتين متساويتين، وهما، ب ج، ه ن.
لنصل، أ د.
أقول:
إن خطي، أ د، ب ن، متوازيان.
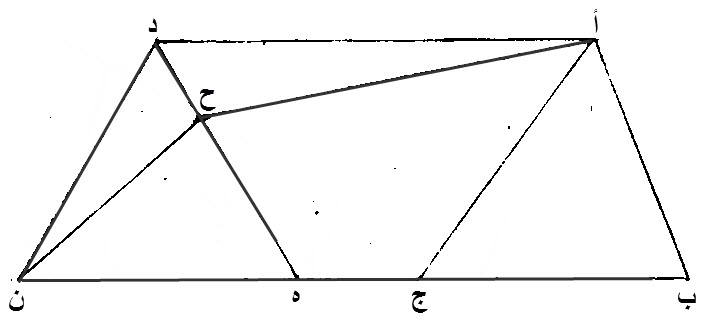
برهان ذلك:
إن لم يكن كذلك، فليكن، أ ح، موازيا، ل، ب ن، إن أمكن ذلك.
نصل، ح ن.
مثلث، أ ب ج، مساو، لمثلث، ح ه ن، لأنهما، على قاعدتي، ب ج، ه ن، المتساويتين، وفيما بين خطي، أ ح، ب ن، المتوازيين.
مثلث، أ ب ج، مساو، لمثلث، د ه ن.
مثلث، د ه ن، مساو، لمثلث، ح ه ن.
الأعظم، الأصغر، ذلك، غير ممكن.
ليس، أ ح، بمواز، ل، ب ن.
كذلك أيضا، نبين، أنه ليس يخرج، خط، مواز، لخط، ب ن، سوى، أ د.
أ د، مواز، ل، ب ن.
فالمثلثات، المتساوية، التي، على قواعد متساوية، وقواعدها، على خط مستقيم، وفي جهة واحدة، هي، فيما بين خطوط، بأعيانها، متوازية.
ذلك، ما أردنا، أن نبين.
٤١ - إذا كان، سطح، متوازي الاضلاع، ومثلث، على قاعدة واحدة، وفيما بين خطين، بأعيانها متوازيين، فإن السطح، المتوازي الاضلاع، مثلا، المثلث.
ليكن، السطح، المتوازي الأضلاع، أ د ج ب، والمثلث، ه ب ج.
هما، على قاعدة واحدة، هي، ب ج، وفيما بين خطي، أ ه، ب ج، المتوازيين.
أقول:
إن سطح، أ د ج ب، المتوازي الاضلاع، مثلا، مثلث، ه ب ج.
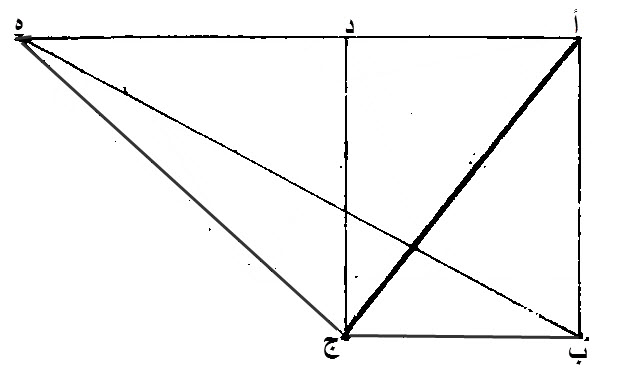
برهان ذلك:
لنوصل، خط، أ ج.
مثلث، أ ب ج، مساو، لمثلث، ه ب ج، لأنهما، على قاعدة واحدة، وهي، ب ج، وفيما بين خطي، أ ه، ب ج، المتوازيين.
مثلث، أ ب ج، هو نصف سطح، أ د ج ب، المتوازي الاضلاع، لأن قطره، أ ج.
يكون، سطح، أ د ج ب، المتوازي، مثلي، مثلث، ه ب ج.
فإذا كان، سطح، متوازي الاضلاع، ومثلث، على قاعدة واحدة، وفيما بين خطين، بأعيانها متوازيين، فإن السطح، المتوازي الاضلاع، مثلا، المثلث.
ذلك، ما أردنا، أن نبين.
٤٢ - أن نقيم، سطحا، متوازي الاضلاع، مساويا، لمثلث مفروض، مساوية زاويته، لزاوية مفروضة، مستقيمة الخطين.
ليكن، المثلث، المفروض، أ ب ج.
لتكن، الزاوية، المفروضة، المستقيمة الخطين، زاوية، د.
ينبغي:
أن نقيم، سطحا، متوازي الاضلاع، مساويا، لمثلث، أ ب ج، المفروض، مساوية زاويته، لزاوية، د، المستقيمة، الخطين.
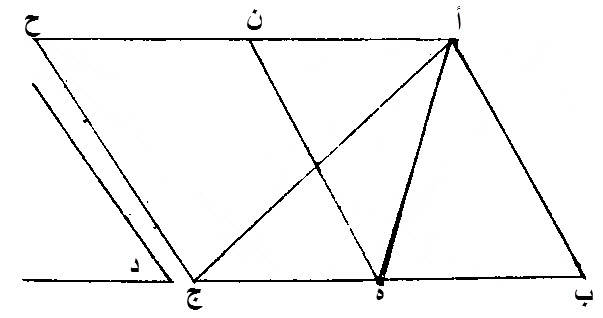
نقسم، ب ج، بنصفين، على نقطة، ه.
نصل، أ ه.
نقيم، على خط، ه ج، المستقيم، على نقطة، ه، منه، زاوية، مستقيمة الخطين، مساوية، لزاوية، د، المستقيمة الخطين، وهي زاوية، ن ه ج.
نخرج، من نقطة، ج، خط، ح ج، موازيا، لخط، ن ه، المستقيم.
نخرج، من نقطة، أ، خطا، موازيا، لخط، ب ج، المستقيم، وهو، أ ح.
مثلث، أ ب ه، مساو، لمثلث، أ ه ج، لانهما، على قاعدتي، ب ه، ه ج، المتساويتين، وفيما بين خطي، أ ح، ب ج، المتوازيين.
مثلث، أ ب ج، مثلا، مثلث، أ ه ج.
سطح، ن ح ج ه، المتوازي الاضلاع، مثلا، مثلث، أ ه ج، لأنهما، على قاعدة واحدة، وهي، ه ج، وفيما بين، خطي، أ ح، ه ج، المتوازيين.
الأشياء التي هي، مثلان، لشيء واحد، بعينه، هي، متساوية.
سطح، ن ح ج ه، المتوازي الاضلاع، مساو، لمثلث، أ ب ج.
قد أقيم، سطح، ن ح ج ه، المتوازي الاضلاع، مساو، لمثلث، أ ب ج، وزاوية، ن ه ج، منه، مساوية، لزاوية، د.
ذلك، ما أردنا، أن نبين.
٤٣ - كل سطح، متوازي الاضلاع، فإن السطحين، المتوازيين الاضلاع، الذين، عن جنبي قطره، الذين، يقال لهما، المتممان، متساويان.
ليكن، سطح، متوازي الاضلاع، عليه، ج د أ ب.
ليكن، قطره، د ب.
ليكن، على قطر، د ب، سطحا، ح د ه ن، ك ن ط ب، المتوازيا، الاضلاع.
ليكن، للذين، يقال لهما، المتممان، سطحا، ن ه أ ط، ج ح ن ك.
أقول:
إن متمم، ن ه أ ط، مساو، لمتمم، ج ح ن ك.
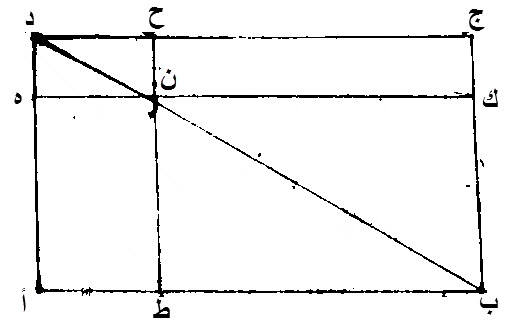
برهان ذلك:
سطح، ج د أ ب، متوازي الاضلاع.
قطره، د ب.
مثلث ج د ب، مساو، لمثلث، د ب أ.
سطح، ح د ه ن، متوازي الاضلاع.
قطره، د ن.
مثلث، ح د ن، مساو، لمثلث، د ن ه.
كذلك أيضا، مثلث، ك ن ب، مساو، لمثلث، ن ب ط.
مثلثا، ك ن ب، ح د ن، مساويان، لمثلثي، ن ب ط، د ن ه.
جميع، مثلث، ج د ب، مساو، لجميع، مثلث، د ب أ.
إذا، نقص، المثلثات، الأربعة، المتساوية، بقي، سطح، ج ح ن ك، المتمم، مساويا، لسطح، ن ه أ ط، المتمم، الباقي.
فكل سطح، متوازي الاضلاع، فإن السطحين، المتوازيين الاضلاع، الذين، عن جنبي قطره، الذين، يقال لهما، المتممان، متساويان.
ذلك، ما أردنا، أن نبين.
٤٤ - أن نعمل، على خط، مستقيم، مفروض، سطحا، متوازي الاضلاع، مساو، لمثلث، مفروض، مساوية زاويته، لزاوية، مفروضة، مستقيمة، الخطين.
ليكن، الخط، المستقيم، المفروض، ب أ.
ليكن، المثلث، المفروض، ج د ه.
لتكن الزاوية، المفروضة، المستقيمة، الخطين، زاوية، ر.
ينبغي:
أن نعمل، على، ب أ، المستقيم، المفروض، سطحا، متوازي الاضلاع، مساو، لمثلث، ج د ه، المفروض، مساوية زاويته، لزاوية، ر، المستقيمة الخطين.
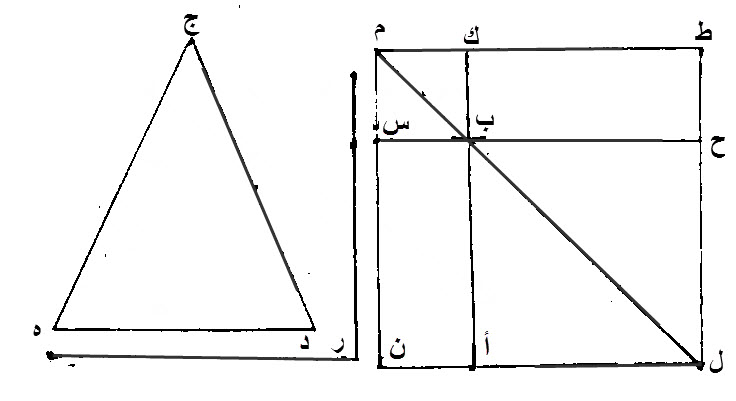
ليقام، سطح، متوازي الاضلاع، عليه، ط ك ب ح، مساو، لمثلث، ج د ه، المفروض، مساوية زاويته، لزاوية، ر.
ليكن، ك ب، منه، على استقامة، أ ب.
نتم، سطح، ح ب أ ل، المتوازي الاضلاع.
نصل، خط، ب ل.
خط، ط ل، مواز، لخط، ك أ، وقد وقع، عليهما، خط، ب ل، المستقيم.
زاويتا، ط ل ب، ك ب ل، الداخلتان، مساويتان، لقائمتين.
زاويتا، ط ل ب، ك ب ح، أقل، من قائمتين.
زاوية، ك ب ح، مثل، زاوية، ك ط ح.
زاويتا، ط ل ب، ك ط ل، أقل، من زاويتين قائمتين.
الخطوط، التي تخرج، من أقل، من زاويتين قائمتين، إلى ما لا نهاية، تلتقي.
خطا، ط ك، ل ب، إذا خرجا، الى ما لا نهاية، إلتقيا.
ليخرجا، وليلتقيا، على نقطة، م.
نخرج، من نقطة م، خطا، موازيا، لخطي، ط ل، ك أ.
نخرج، خطي، ب س، أ ن، على إستقامة، خطي، ح ب، ل أ.
ط م، مواز، ل، ل ن.
سطح، ط م ن ل، متوازي الاضلاع.
قطره، خط، م ل.
على قطر، م ل، سطحا، ك م س ب، ح ب أ ل، المتوازيا الاضلاع.
سطحا، ط ك ب ح، ب س ن أ، هما، المتممان.
سطح، ط ك ب ح، المتوازي الاضلاع، مساو، لسطح، ب س ن أ، المتوازي الاضلاع.
سطح، ط ك ب ح، مساو، لمثلث، ج د ه.
سطح، ب س ن أ، المتوازي الاضلاع، مساو، لمثلث، ج د ه.
زاوية، أ ب س، مساوية، لزاوية، ر.
قد عمل، على خط، أ ب، المستقيم، المفروض، سطح، ب س ن أ، المتوازي الاضلاع، مساو، لمثلث، ج د ه، المفروض، وزاوية، أ ب س، منه، مساوية، لزاوية، ر المفروضة، المستقيمة، الخطين.
ذلك، ما أردنا، أن نبين.
٤٥ - أن نقيم، على خط، مستقيم، مفروض، سطحا، متوازي الاضلاع، مساويا، لشكل، مستقيم الخطوط، مساوية زاويته، لزاوية، مفروضة، مستقيمة الخطين.
ليكن، الخط، المستقيم، المفروض، خط، ه ط.
ليكن، الشكل، المستقيم الخطوط، المفروض، أ ج د ب.
لتكن، الزاوية، المفروضة، المستقيمة الخطين، زاوية، ل.
ينبغي:
أن نقيم، على، ه ط، سطحا، متوازي الاضلاع، مساو، لشكل، أ ج د ب.
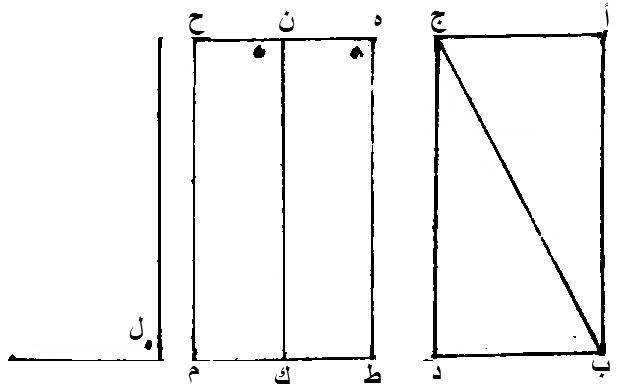
نصل، ج ب.
نعمل، على خط، ه ط، شكلا، متوازي الاضلاع، مساويا، لمثلث، أ ج ب، وهو، ه ن ك ط، مساوية، زاوية، ن ه ط، منه، لزاوية، ل.
نعمل، على، ن ك، سطحا، متوازي الاضلاع، مساويا، لمثلث، ج ب د، وهو، ن ح م ك، مساوية، زاوية، ح ن ك، منه، لزاوية، ل.
كل واحدة، من زاويتي، ن ه ط، ح ن ك، مساوية، لزاوية، ل.
زاوية، ن ه ط، مساوية، لزاوية، ح ن ك.
نجعل، زاوية، ه ن ك، مشتركة.
زاويتا، ه ن ك، ن ه ط، متساويتين، لزاويتي، ه ن ك، ح ن ك.
زاويتا، ه ن ك، ن ه ط، مساويتين، لقائمتين.
زاويتا، ه ن ك، ح ن ك، مساويتان، لقائمتين.
خط، ه ن، على إستقامة، خط، ن ح.
كذلك أيضا، يكون، خط، ط ك، على إستقامة، خط، ك م.
ه ن، مساو، ل، ط ك، ومواز له.
ن ح، مساو، ل، ك م، ومواز له.
جميع، ه ح، مساو، ل، ط م، ومواز له.
ه ط، مساو، ل، ح م.
سطح، ه ح م ط، متوازي الاضلاع.
مثلث، أ ج ب، مساو، لسطح، ه ن ك ط، المتوازي.
مثلث، ج ب د، مساو، لسطح، ن ح م ك.
جميع سطح، ه ح م ط، المتوازي الاضلاع، مساو، لشكل، أ ج د ب، المستقيم الخطوط.
زاوية، ه، منه، مساوية، لزاوية، ل.
ذلك، ما أردنا، أن نبين.
٤٦ - أن نعمل، على خط مستقيم، مفروض، مربعا، قائم الزوايا.
ليكن، الخط، المفروض، المستقيم، أ ب.
ينبغي:
أن نعمل عليه، مربعا.
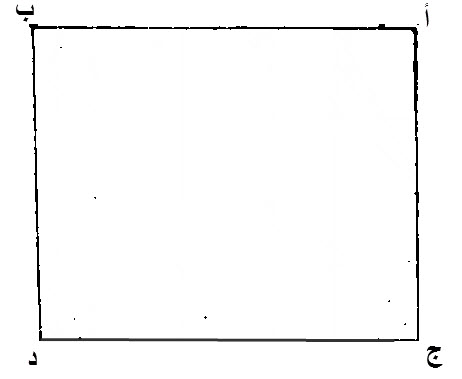
نخرج، من خط، أ ب، من نقطة، أ، منه، خطا مستقيما، على زاوية قائمة، وهو خط، أ ج.
نجعل، أ ج، مثل، أ ب.
نخرج، من نقطة، ج، خطا، مستقيما، موازيا، لخط، أ ب، وهو، ج د.
نخرج، من نقطة، ب، خطا، موازيا، لخط، أ ج، وهو، ب د.
سطح، أ ب د ج، متوازي الاضلاع.
خط، أ ب، مساو، لخط، ج د.
خط، أ ج، مساو، لخط، ب د.
خط أ ب، مساو، لخط، أ ج.
خط، أ ج، مساو، لخط، ج د.
خط، أ ب، مساو، لخط، ب د.
خطوط، أ ب، أ ج، ب د، ج د، الأربعة، متساوية.
سطح، أ ب د ج، متساوي الاضلاع.
أقول، إنه، قائم الزوايا.
قد وقع، على خط، أ ب، ج د، المتوازيين، خط، أ ج.
زاويتا، ب أ ج، أ ج د، مساويتين، لقائمتين.
زاوية، ب أ ج، قائمة.
زاوية، أ ج د، أيضا، قائمة.
الزوايا، والاضلاع، المتقابلة، من السطوح، المتوازية، الاضلاع، هي متساوية.
كل واحدة، من زاويتي، أ ب د، ب د ج، المتقابلتين، للزاويتين التين ذكرنا، قائمة.
سطح، أ ب د ج، قائم، الزوايا.
قد تبين، أنه متساوي الاضلاع.
سطح، أ ب د ج، مربع، وهو معمول، على خط، أ ب، المفروض، مربعا.
ذلك، ما أردنا، أن نبين.
٤٧ - المربع، الكائن، من الضلع، الذي يوتر، الزاوية القائمة، من المثلثات، القائمة الزوايا، مساو، للمربعين، الكائنين، من الضلعين، المحيطين، بالزاوية القائمة.
ليكن، المثلث، القائم الزوايا، أ ب ج.
لتكن، زاويته، القائمة، ب أ ج.
أقول:
المربع الكائن، من، ب ج، مثل، المربعين، الكائنين، من ضلعي، أ ب، أ ج.
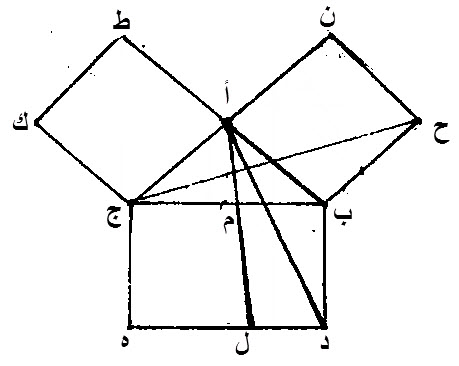
برهان ذلك:
نعمل، على خط، ب ج، مربع، هو، ب ج ه د.
نعمل، على خطي، أ ب، أ ج، مربعي، ن أ ب ح، ط ك ج أ.
نخرج، من نقطة، أ، خط، أ ل، مواز، لكل واحد، من خطي، ب د، ج ه.
نصل، خطي، ح ج، أ د.
زاوية، ن أ ب، قائمة.
زاوية، ب أ ج، قائمة.
يكون، قد أخرج، من خط ما، وهو أ ب، من نقطة، أ منه، خطا، أ ن، أ ج، المستقيمان، وليسا في جهة واحدة، فيصير، زاويتي، ن أ ب، ب أ ج، اللتين، عن الجنبين، متساويتين، لقائمتين، فخط، ن أ، على إستقامة، خط، أ ج.
كذلك، خط، ط أ، على إستقامة، خط، أ ب.
زاوية، ح ب أ، مساوية، لزاوية، ج ب د، وذلك، أن كل واحدة، منهما، قائمة.
نجعل، زاوية، أ ب ج، مشتركة، فيكون، جميع زاوية، ح ب ج، مساوية، لجميع، زاوية، أ ب د.
ح ب، مساو، ل، أ ب.
ب ج، مساو، ل، ب د.
كلي خطي، ح ب، ب ج، مساويين، لكلي خطي، أ ب، ب د، كل واحد لنظيره، وزاوية، ح ب ج، مساوية، لزاوية، أ ب د.
قاعدة، ح ج، مساوية، لقاعدة، أ د.
مثلث، ح ب ج، مساو، لمثلث، أ ب د.
سطح، ب م ل د، المتوازي الاضلاع، مثلا، مثلث، أ ب د، لانهما، على قاعدة واحدة، وهي، ب د، وفيما بين، خطي، ب د، أ ل، المتوازيين.
سطح، ن أ ب ح، المتوازي الاضلاع، مثلا، مثلث، ح ب ج، لانهما، على قاعدة واحدة، وهي، ح ب، وفيما بين خطي، ح ب، ن أ، المتوازيين.
التي، هي ضعف، لأشياء متساوية، فهي أيضا، متساوية.
سطح، ب م ل د، المتوازي الاضلاع، مساو، لمربع، ن أ ب ح.
كذلك، سطح، م ج ه ل، مساو، لمربع، أ ط ج ك.
فجميع، مربع، ب ج ه د، مساو، لمربعي، ن أ ب ح، ط ك ج أ.
اما مربع، ب ج ه د، فهو الكائن، من، ب ج.
أما مربعا، ن أ ب ح، ط ك ج أ، فهما الكائنان، من، أ ب، أ ج.
المربع، الكائن من، ب ج، مساو، للمربعين، الكائنين، من، أ ب، أ ج.
فالمربع، الكائن، من الضلع، الذي يوتر، الزاوية القائمة، من المثلثات، القائمة الزوايا، مساو، للمربعين، الكائنين، من الضلعين، المحيطين، بالزاوية القائمة.
ذلك، ما أردنا، أن نبين.
٤٨ - إذا كان المربع، الكائن، من ضلع، من أضلاع مثلث، مساويا، للمربعين الكائنين، من الضلعين الباقيين، فإن الزاوية، التي يحيط بها، ذانك، الضلعان الباقيان، من المثلث، قائمة.
ليكن مثلث، عليه، ج ب أ.
ليكن المربع، الكائن، من، ج ب، منه، مساويا، للمربعين الكائنين، من، ج أ، ب أ.
أقول:
إن زاوية، ج أ ب، قائمة.
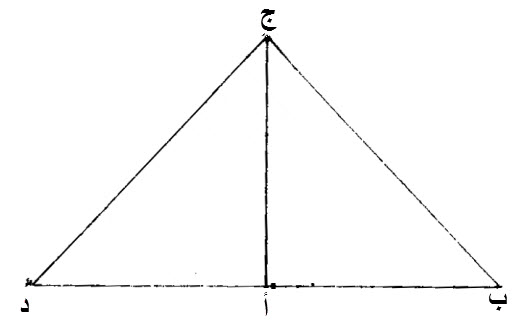
برهان ذلك:
نخرج، من نقطة، أ، خط، أ د، على زاوية قائمة، مساويا، لخط، أ ب.
نصل، خط، ج د.
مربع، ج ب، مساو، للمربعين، الكائنين، من، ج أ، ب أ.
خط، ب أ، مساو، لخط، أ د.
المربع، الكائن من، ج ب، مساو، للمربعين الكائنين، من، ج أ، أ د.
هما، مساويان للمربع، الكائن من، ج د، لأن، زاوية، ج أ د، قائمة.
المربع، الكائن، من، ج د، مساو، للمربع، الكائن، من، ج ب.
خط، ج ب، مساو، لخط، ج د.
خط، ب أ، مساو، لخط، أ د.
نجعل، خط، ج أ، مشتركا.
كلي، خطي، ج أ، ب أ، مساويين، لكلي خطي، ج أ، أ د، كل واحد، لنظيره، وقاعدة، ج ب، مساوية، لقاعدة، ج د.
زاوية، ج أ ب، قائمة.
فإذا كان المربع، الكائن، من ضلع، من أضلاع مثلث، مساويا، للمربعين الكائنين، من الضلعين الباقيين، فإن الزاوية، التي يحيط بها، ذانك، الضلعان الباقيان، من المثلث، قائمة.
وذلك ما أردنا أن نبين.
تمت، المقالة الأولى، من كتاب أوقليدس، في الأصول، ثابت بن قرة، ولله الحمد كثيرا.