الخوارزمي، هو عالم رياضيات عربي، ولد في القرن الثاني بعد الهجرة.
ألف كتابه المختصر في حساب الجبر والمقابلة، بتشجيع من المأمون، وذلك لما يلزم الناس، من الحاجة إليه في مساحة الأرضين، كري الأنهار، الهندسة، و في مواريثهم، ومقاسمتهم وتجاراتهم، و غير ذلك من جوه ما يتعاملون به.
الحمد لله على نعمه، بما هو أهله من محامده، التي بأداء ما افترض منها على من يعبده من خلقه، يقع اسم الشكر، ويستوجب المزيد، ونؤمن من الغير، اقراراً بربوبيته، وتذللا لعزته، وخشوعاً لعظمته.
بعث محمداً، صلى الله عليه وعلى آله وسلم، بالنبوة، على حين فترة من الرسل، وتنكر من الحق، ودروس من الهدى، فبصر به من العمى، واستنقذ به من الهلكة، وكثر به بعد القلة، والف به بعد الشتات.
تبارك الله ربنا، وتعالى جده، وتقدست اسماؤه، ولا إله غيره، وصلى الله على محمد النبي، وآله وسلم.
ولم تزل العلماء، في الأزمنة الخالية، والأمم الماضية، يكتبون الكتب، مما يصنفون من صنوف العلم، ووجوه الحكمة، نظراً لمن بعدهم، واحتساباً للأجر بقدر الطاقة، ورجاء أن يلحقهم من أجر ذلك، وذخره، وذكره، ويبقى لهم من لسان الصدق، ما يصغر في جنبه، كثير مما كانوا يتكلفونه، من المؤونة، ويحملونه على أنفسهم من المشقة، في كشف أسرار العلم وغامضه.
إما رجل، سبق إلى ما لم يكن مستخرجاً قبله، فورثه من بعده.
إما رجل، شرح مما أبقى الأولون، ما كان مستغلقاً، فأوضح طريقه، وسهل مسلكه، وقرب مأخذه.
إما رجل، وجد في بعض الكتب خللا، فلَمَّ شعثه، وأقام أدده، وأحسن الظن بصاحبه، غير راد عليه، ولا مفتخر من ذلك، بفعل نفسه.
وقد شجعني، ما فضل الله به الامام المأمون، أمير المؤمنين، مع الخلافة التي حاز له إرثها، وأكرمه بلباسها، وحلاه بزينتها، من الرغبة في الأدب، وتقريب أهله وادنائهم، وبسط كنفه لهم، ومعونته إياهم على إيضاح ما كان مستبهماً، وتسهيل ما كان مستوعراً، على أن ألفت من حساب الجبر والمقابلة، كتاباً مختصراً حاصراً، للطيف الحساب وجليله، لما يلزم الناس، من الحاجة إليه في مواريثهم، ووصاياهم، وفي مقاسمتهم، وأحكامهم، وتجاراتهم، وفي جميع ما يتعاملون به بينهم، من مساحة الأرضين، وكري الأنهار، والهندسة، وغير ذلك من وجوهه وفنونه، مقدمًا لحسن النية فيه، وراجيًا لأن ينزله أهل الأدب، بفضل ما استودعوا من نعم الله تعالى، وجليل آلائه، وجميل بلائه، عندهم منزلته.
بالله توفيقي، في هذا وفي غيره، عليه توكلت وهو رب العرش العظيم، وصلى الله على جميع الأنبياء والمرسلين.
إني لما نظرت فيما يحتاج إليه الناس من الحساب، وجدت جميع ذلك عدداً، ووجدت جميع الأعداد إنما تركبت من الواحد، والواحد داخل في جميع الأعداد.
ووجدت جميع ما يلفظ به من الأعداد، ما جاوز الواحد إلى العشرة، يخرج مخرج الواحد، ثم تثنى العشرة، وتثلث، كما فعل بالواحد، فتكون منها العشرون والثلاثون إلى تمام المائة.
ثم تثنى المائة، وتثلث، كما فعل بالواحد، وبالعشرة، إلى الألف، ثم كذلك تردد الألف، عند كل عقد، إلى غاية المدرك من العدد.
ووجدت الأعداد، التي يحتاج إليها في حساب الجبر والمقابلة، على ثلاثة ضروب، وهي: جذور، أموال، وعدد مفرد، لا ينسب إلى جذر، ولا إلى مال.
- الجذر منها، كل شيء مضروب في نفسه، من الواحد، وما فوقه من الأعداد، وما دونه من الكسور.
- المال، كل ما اجتمع من الجذر، المضروب في نفسه.
- العدد المفرد، كل ملفوظ به من العدد، بلا نسبة إلى جذر، ولا إلى مال.
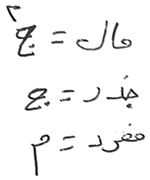
٢ - الأبواب الستة لحساب الجبر والمقابلة
من هذه الضروب الثلاثة، ما يعدل بعضهم بعضاً، وهو كقولك:
- أموال تعدل جذوراً.
- أموال تعدل عدداً.
- جذور تعدل عدداً.
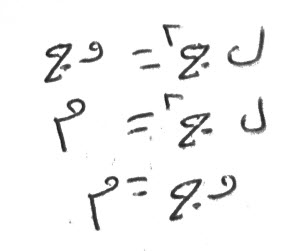
فأمّا الأموال التي تعدل الجذور، فمثل قولك:
- مال يعدل خمسة أجذاره، فجذر المال خمسة، والمال خمسة وعشرون، وهو مثل خمسة أجذاره.
- ثلث مال، يعدل أربعة أجذار، فالمال كله، يعدل أثني عشر جذراً، وهو مائة وأربعة وأربعون، وجذره أثني عشر.
- خمسة أموال، تعدل عشرة أجذار، فالمال الواحد، يعدل جذرين، وجذر المال اثنان، والمال أربعة.
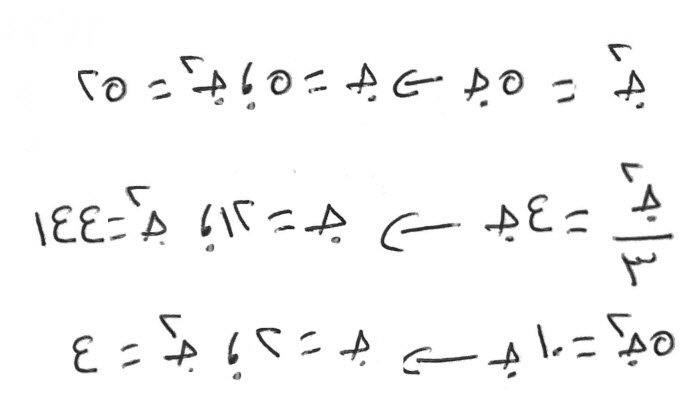
كذلك، ما كثر من الأموال، أو قل، يرد إلى مال واحد، كذلك يفعل، بما عادلها من الأجذار، يرد إلى مثل ما يرد إليه المال.
أمّا الأموال، التي تعدل العدد، فمثل قولك:
- مال يعدل تسعة، فهو المال، وجذره ثلاثة.
- خمسة أموال تعدل، ثمانين، فالمال الواحد خمس الثمانين، وهو ستة عشر.
- نصف مال، يعدل ثمانية عشر، فالمال يعدل ستة وثلاثين، وجذره ستة.
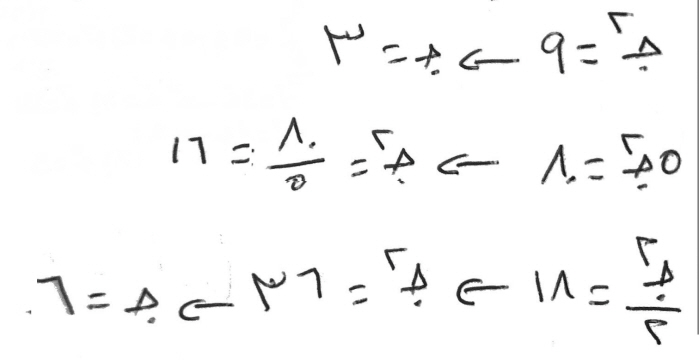
كذلك، جميع الأموال، زائدها وناقصها، ترد إلى مال واحد، وإن كانت أقل من مال، زيد عليها تكمل مالا تاما، وكذلك يفعل، بما عادلها من الأعداد.
وأمّا الجذور، التي تعدل عدداً، فكقولك:
- جذر يعدل ثلاثة من العدد، فالجذر ثلاثة، والمال الذي يكون منه تسعة.
- أربعة أجذار تعدل عشرين، فالجذر الواحد يعدل خمسة، والمال الذي يكون منه، خمسة وعشرون.
- نصف جذر يعدل عشرة، فالجذر يعدل عشرين، والمال الذي يكون منه أربعمائة.
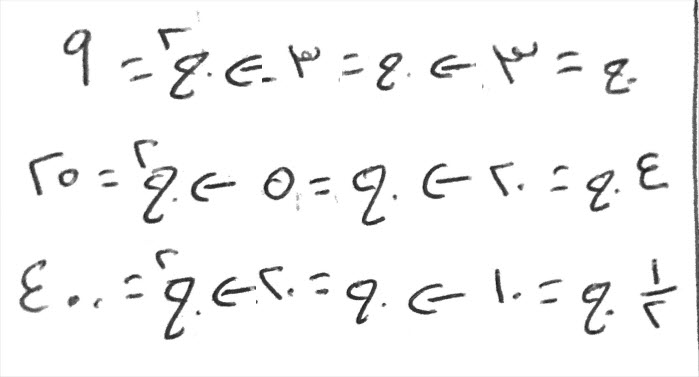
ووجدت هذه الضروب الثلاثة، التي هي الجذور، والأموال، والعدد، تقترن، فيكون منها، ثلاثة اجناس مقترنة، وهي:
- أموال وجذور، تعدل عدداً.
- أموال وعدد، تعدل جذوراً.
- جذور وعدد، تعدل اموالاً.
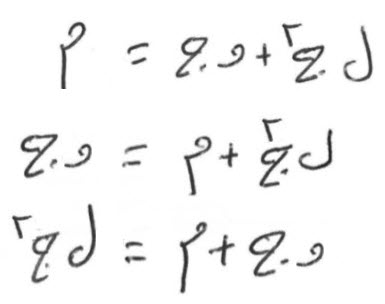
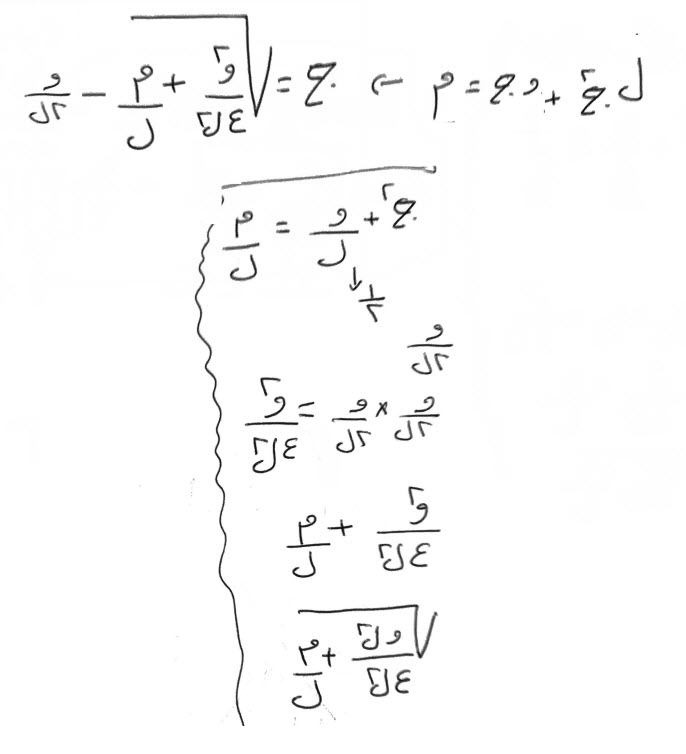
فأما الأموال، والجذور، التي تعدل العدد، فمثل قولك:
مال، وعشرة أجذاره، يعدل تسعة وثلاثين درهماً. معناه، أيّ مال، إذا زدت عليه، مثل عشرة أجذاره، بلغ ذلك كله تسعة وثلاثين.
بابه، أن تنصف الأجذار، وهي في هذه المسألة خمسة، فتضربها في مثلها، فتكون خمسة وعشرين، فتزيدها على التسعة والثلاثين، فتكون أربعة وستين، فتأخذ جذرها، وهو ثمانية، فتنقص منه نصف الأجذار، وهو خمسة، فيبقى ثلاثة، وهو جذر المال الذي تريد، والمال تسعة.
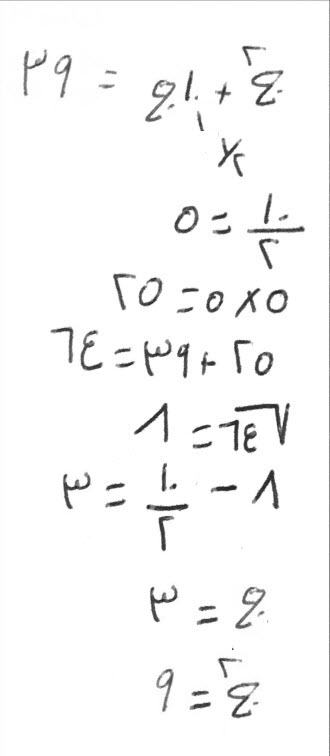
كذلك، لو ذكر مالين، أو ثلاثة، أو أقل أو أكثر، فأردده إلى مال واحد، واردد ما كان معه من الأجذار، والعدد، إلى مثل ما رددت إليه المال.
وهو نحو قولك، مالان، وعشرة أجذار، تعدل ثمانية وأربعين درهماً.
معناه، أي مالين إذا جمعا، وزيد عليهما مثل عشرة أجذار أحدهما، بلغ ذلك ثمانية وأربعين درهماً.
ينبغي أن ترد المالين إلى مال واحد، وقد علمت أن مالاً، من مالين نصفهما، فأردد كل شيء في المسألة إلى نصفه، فكأنه قال، مال، وخمسة أجذار، يعدل أربعة وعشرين درهماً.
معناه، أي مال، إذا زدت عليه خمسة أجذاره، بلغ ذلك أربعة وعشرين.
فنصف الأجذار، فتكون اثنين ونصفا، فاضربها في مثلها، فتكون ستة وربعا، فزدها على الأربعة والعشرين، فتكون ثلاثين درهماً وربعا.
خذ جذرها، وهو خمسة ونصف، فانقص منها نصف الأجذار، وهو اثنان ونصف، يبقى ثلاثة، وهو جذر المال، والمال تسعة.
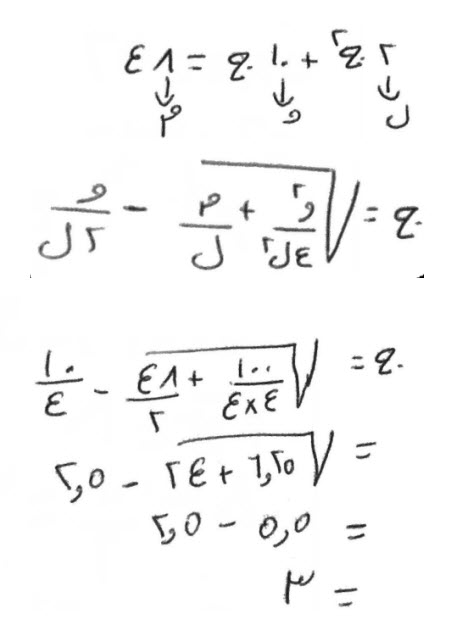
كذلك لو قال، نصف مال، وخمسة أجذاره، يعدل ثمانية وعشرين درهماً.
عنى ذلك، أي مال، إذا زدت على نصفه، مثل خمسة أجذاره، بلغ ذلك، ثمانية وعشرين درهماً.
تكمل مالك، حتى يبلغ مالاً تاماً، وهو أن تضعفه.
أضعفه، وأضعف كلما معك، مما يعادله، فيكون، مالاً وعشرة أجذار، يعدل ستة وخمسين درهماً.
نصف الأجذار تكون خمسة، اضربها في مثلها تكون خمسة وعشرين، زدها على الستة والخمسين تكون احدا وثمانين، خذ جذرها وهو تسعة، انقص منها نصف الأجذار وهو خمسة، يبقى أربعة، وهو جذر المال الذى أردته، والمال ستة عشر، ونصفه ثمانية.
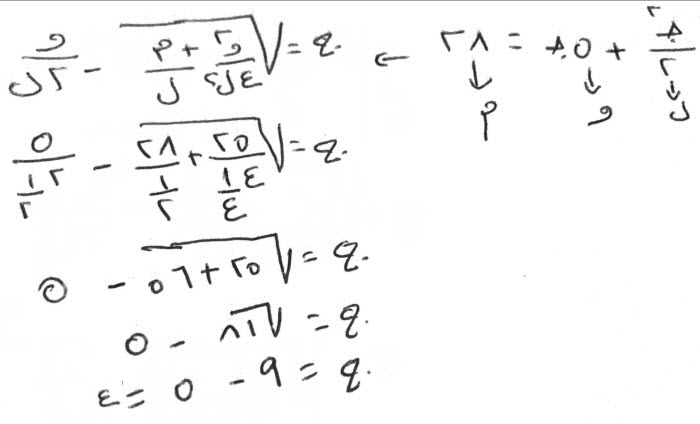
كذلك فافعل، بجميع ما جاءك من الأموال والجذور، وما عادلها من العدد، تصب إن شاء الله.
وأمّا الأموال والعدد، التي تعدل الجذور،
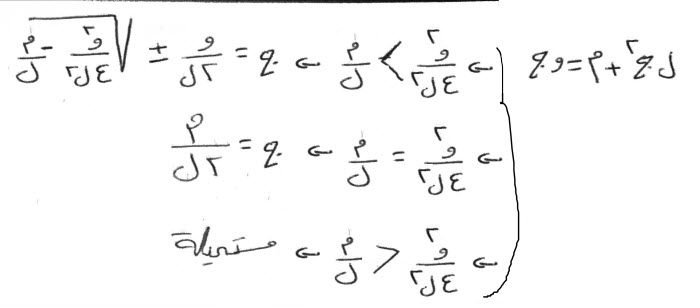
فنحو قولك:
مال وواحد وعشرون من العدد، يعدل عشرة أجذاره. معناه، أي مال، إذا زدت عليه واحدا وعشرين درهماً، كان ما اجتمع، مثل عشرة أجذار ذلك المال.
بابه، أن تنصف الأجذار، فتكون خمسة. اضربها في مثلها، يكون خمسة وعشرين. أنقص منها الواحد والعشرين، التي ذكر انها مع المال، فيبقى أربعة، فخذ جذرها، وهو اثنان، فأنقصه من نصف الأجذار، وهو خمسة، فيبقى ثلاثة، وهو جذر المال الذي تريده، والمال تسعة.
وإن شئت، فزد الجذر، على نصف الأجذار، فتكون سبعة، وهو جذر المال الذي تريده، والمال تسعة وأربعون.
فإذا وردت عليك مسألة، تخرجك إلى هذا الباب، فامتحن صوابها بالزيادة، فان لم تكن، فهي بالنقصان لا محالة.
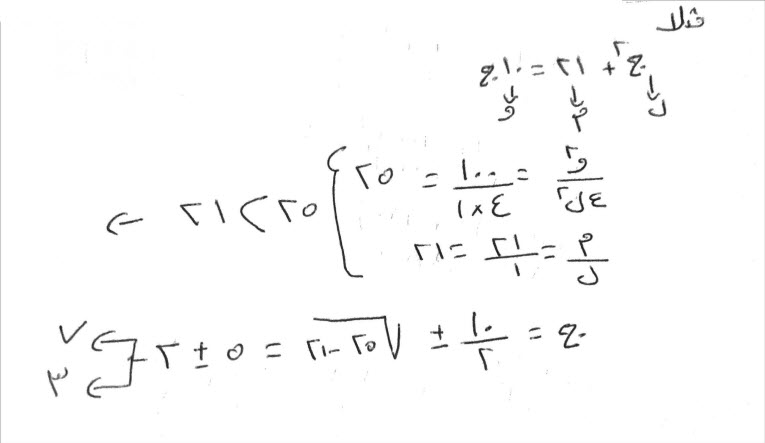
وهذا الباب يعمل بالزيادة والنقصان جميعاً، وليس ذلك في غيره من الأبواب الثلاثة، التي يحتاج فيها إلى تنصيف الأجذار.
إعلم، أنك إذا نصفت الأجذار في هذا الباب، وضربتها في مثلها، فكان:
- مبلغ ذلك، أقل من الدراهم التي مع المال، فالمسألة مستحيلة.
- إن كان مثل الدراهم بعينها، فجذر المال، مثل نصف الأجذار سواء، لا زيادة ولا نقصان.
وكل ما أتاك من مالين، أو أكثر أو أقل، فأردده إلى مال واحد، كنحو ما بينت لك في الباب الأول.
وأمّا الجذور والعدد، التي تعدل الأموال،
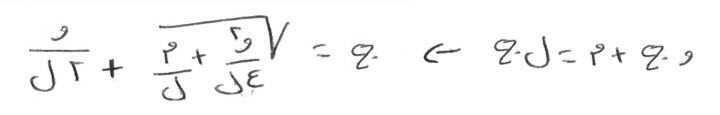
فنحو قولك،
ثلاثة أجذار، وأربعة من العدد، تعدل مالاً.
انصف الأجذار، فتكون واحداً ونصفاً. اضربها في مثلها، فتكون اثنين وربعاً. زدها على الأربعة، فتكون ستة وربعاً. خذ جذرها، وهو اثنان ونصف. زده على نصف الأجذار، وهو واحد ونصف، فتكون أربعة، وهو جذر المال، والمال ستة عشر.
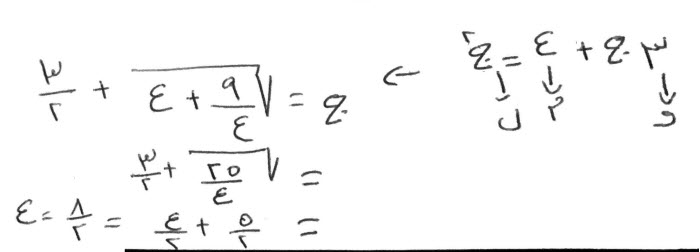
كل ما كان أكثر من مال، أو أقل، فأردده إلى مال واحد.
فهذه الستة الضروب، التي ذكرتها في صدر كتابي هذا، وقد أتيت على تفسيرها، واخبرت أن منها ثلاثة ضروب، لا تنصف فيها الأجذار، وقد بينت قياسها واضطرارها.
فأمّا ما تحتاج فيه إلى تنصيف الأجذار، في الثلاثة الأبواب الباقية، فقد وصفته بأبواب صحيحة، وصيرت لكل باب منها صورة، يستدل منها على العلة في التنصيف.
علة، مال وعشرة أجذار يعدل تسعة وثلاثين درهماً
صورة ذلك، سطح مربع، مجهول الأضلاع، وهو المال الذي تريد أن تعرفه، وتعرف جذره، وهو سطح أ ب.
كل ضلع من أضلاع هذا المربع، هو جذره، وكل ضلع من أضلاعه، إذا ضربته في عدد من الأعداد، فما بلغت الأعداد، فهي أعداد جذور.
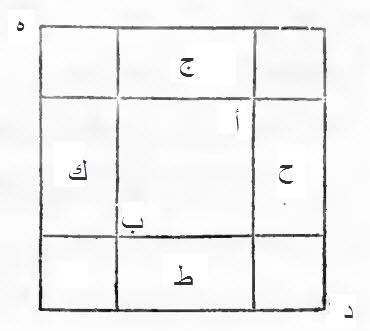
لما قيل إن مع المال، عشرة أجذاره، اخذنا ربع العشرة، وهو اثنان ونصف، وصيرنا كل ربع منها، مع ضلع من أضلاع السطح، فصار مع السطح الأول، الذي هو سطح أ ب، أربعة سطوح متساوية، طول كل سطح منها، مثل جذر سطح أ ب، وعرضه اثنان ونصف.
وهي سطوح، ح، ط، ك، ج.
حدث سطح، متساوي الأضلاع، مجهول أيضاً، ناقص في زواياه الأربع، في كل زاوية من النقصان، اثنان ونصف في اثنين ونصف، فصار الذي يحتاج إليه من الزيادة حتى يتربع السطح، اثنان ونصف في مثله أربع مرات.
مبلغ ذلك جميعه خمسة وعشرون.
علمنا، أن السطح الأول، الذي هو سطح المال، والأربعة السطوح التي حوله، وهي عشرة أجذار، هي تسعة وثلاثون من العدد.
إذا زدنا عليها الخمسة والعشرين، التي هي المربعات الأربع، التي هي على زوايا سطح أ ب، تم تربيع السطح الأعظم، وهو سطح د ه.
علمنا، أن ذلك كله أربعة وستون، وأحد أضلاعه جذره، وهو ثمانية.
إذا نقصنا من الثمانية، مثل ربع العشرة، مرتين من طرفي ضلع السطح الأعظم، الذي هو سطح د ه، وهو خمسة، بقي من ضلعه ثلاثة، وهو جذر ذلك المال.
إنما نصفنا العشرة الأجذار، وضربناها في مثلها، وزدناها على العدد الذي هو تسعة وثلاثون، ليتم لنا بناء السطح الأعظم بما نقص من زواياه الأربع.
فكل عدد، يضرب ربعه في مثله، ثم في أربعة، يكون مثل ضرب نصفه في مثله، فاستغنينا بضرب نصف الأجذار في مثلها، عن الربع في مثله ثم في أربعة.
وله أيضاً، صورة أخرى، تؤدي إلى هذا.
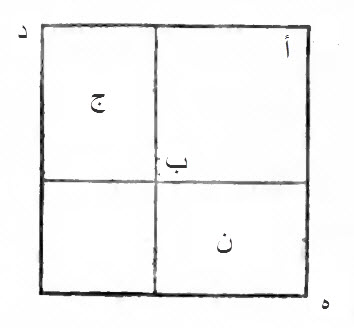
سطح أ ب، هو المال، أردنا أن نزيد عليه مثل عشرة أجذاره، نصفنا العشرة، فصارت خمسة، فصيرناها سطحين، على جنبيّ سطح أ ب، وهما سطحا ج ن.
صار طول كل سطح منهما، خمسة اذرع، وهو نصف العشرة الأجذار، وعرضه مثل ضلع سطح أ ب .
بقيت لنا مربعة من زوايا سطح أ ب، وهي خمسة في خمسة، وهي نصف العشرة الأجذار، التي زدناها على جنبي السطح الأول.
علمنا أن السطح الأول هو المال، وأن السطحين الذين على جنبيه، هما عشرة أجذار، فذلك كله تسعة وثلاثون.
بقي إلى تمام السطح الأعظم، مربع خمسة في خمسة، فذلك خمسة وعشرون.
زدناها على تسعة وثلاثين، ليتم لنا السطح الأعظم، الذي هو سطح د ه.
بلغ ذلك كله أربعة وستين، أخذنا جذرها، وهو ثمانية، وهو أحد أضلاع السطح الأعظم.
إذا نقصنا منه، مثل ما زدنا عليه، وهو خمسة بقي ثلاثة، وهو ضلع سطح أ ب، الذي هو المال، وهو جذره، والمال تسعة.
مال، وإحدى وعشرون درهماً، يعدل عشرة أجذاره
نجعل المال، سطحًا مربعًا، مجهول الأضلاع وهو أ د.
نضم إليه سطحاً متوازي الأضلاع، عرضه، مثل أحد أضلاع سطح أ د، وهو ضلع ه ن، والسطح هو ه ب.
صار طول السطحين جميعاً، ضلع ج ه.
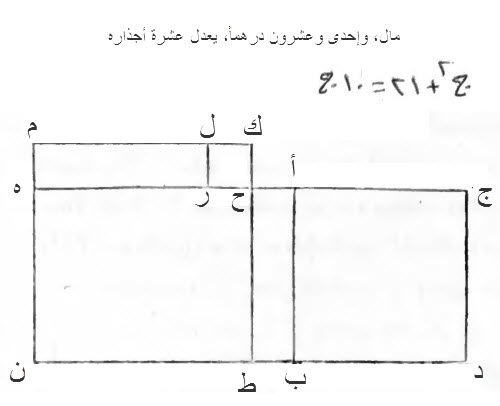
لما قال، مال، وإحدى وعشرون، يعدل عشرة أجذاره، علمنا أن طول ضلع ه ج، عشرة أعداد، لأن ضلع ج د، جذر المال، فأن أحد أضلاعه، مضروباً في واحد، هو جذر ذلك السطح، ومضروباً في أثنين هو جذراه و ...
نقسم ضلع ج ه نصفين، على نقطة ح، خط ه ح، مثل خط ح ج.
خط ح ط، مثل خط ج د.
زدنا على خط ح ط، على استقامته، مثل فضل ج ح، على ح ط، ليتربع السطح.
خط ط ك، مثل خط ك م.
سطح م ط، هو سطح مربع، متساوي الأضلاع، والزوايا.
خط ط ك هو خمسة.
سطح م ط إذاً خمسة وعشرون، وهو ما اجتمع من ضرب نصف الأجذار، في مثلها، وهو خمسة في خمسة، يكون خمسة وعشرين.
سطح ه ب، هو الواحد والعشرون، التي زيدت على المال.
قطعنا من سطح ه ب، بخط ط ك، الذي هو أحد اضلاع سطح م ط، فبقي سطح ط أ.
أخذنا من خط ك م، خط ك ل، وهو مثل خط ح ك.
خط ط ح، مثل خط م ل.
فضل من خط م ك، خط ل ك، وهو مثل خط ك ح.
سطح م ر، مثل سطح ط أ.
سطح ه ط، مزيداً عليه سطح م ر، مثل سطح ه ب وهو واحد وعشرون.
سطح م ط خمسة وعشرين.
ننقص من سطح م ط، سطحي ه ط و م ر، اللذين هما واحد وعشرون، يبقى لنا سطح صغير، وهو سطح ر ك.
سطح ر ك، هو فضل ما بين خمسة وعشرين، وواحد وعشرين، وهو أربعة.
جذرها خط ر ح، وهو مثل خط ح أ، وهو اثنان.
إن نقصتهما من خط ح ج، الذي هو نصف الأجذار، بقي خط أ ج، وهو ثلاثة، وهو جذر المال الأول.
إن زدته على خط ج ح، الذي هو نصف الأجذار، بلغ ذلك سبعة، وهو خط ر ج، ويكون جذر مال، أكثر من هذا المال، إذا زدت عليه واحداً وعشرين، صار ذلك مثل عشرة أجذاره، وذلك ما أردنا أن نبين.
ثلاثة أجذار، وأربعة من العدد، تعدل مالاً
نجعل المال، سطحاً مربعاً، مجهول الأضلاع والزوايا، وهو سطح أ د.
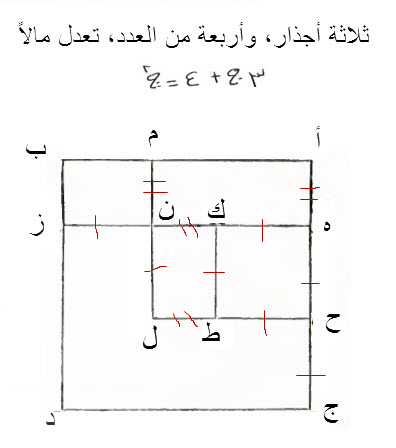
هذا السطح كله، يجمع الثلاثة الأجذار، والأربعة التي ذكرناها.
كل سطح مربع، فأن أحد أضلاعه، في واحد، جذره.
قطعنا من سطح أ د، سطح ه د، وجعلنا أحد أضلاعه، الذي هو ه ج الثلاثة، التي هي عدد الأجذار، والتي هي مثل ز د.
سطح ه ب، هو الأربعة المزيدة على الأجذار.
قطعنا ه ج، الذي هو ثلاثة أجذار، بنصفين، على نقطة ح.
جعلنا منه سطحاً مربعاً، وهو سطح ه ط، وهو ما كان من ضرب نصف الأجذار، الذي هو واحد ونصف، في مثله، وهو اثنان وربع.
زدنا في خط ح ط، مثل أ ه، وهو خط ط ل.
خط ح ل، مثل خط أ ح، وخط ك ن، مثل خط ط ل.
حدث سطح، مربع، متساوي الأضلاع والزوايا، وهو سطح َح م.
خط أ ح، مثل خط م ل.
خط أ ح، مثل خط ح ل.
خط ح ج، مثل خط ن ز.
خط م ن، مثل ط ل.
يفضل من سطح ه ب، مسطح ب ن، مثل سطح ك ل.
سطح أ ز، هو الأربعة الزائدة، على الثلاثة الأجذار.
سطح أ ن، وسطح ك ل، مثل سطح أ ز، الذي هو الأربعة العدد.
سطح ح م، هو: نصف الأجذار، الذي هو واحد ونصف، في مثله، وهو اثنان وربع، وزيادة، الأربعة التي هي سطح أ ن، وسطح ك ل.
أ ح، هو جذر سطح ح م، وهو اثنان ونصف.
ح ج، هو نصف الثلاثة الأجذار، وهو واحد ونصف.
إذا زدنا على خط أ ح، وهو اثنان ونصف، خط ح ج، الذي هو واحد ونصف، بلغ ذلك كله أربعة.
خط أ ج هو جذر المال، الذي هو سطح أ د.
ووجدنا، ان كل ما يعمل به من حساب الجبر والمقابلة، لابد أن يخرجك إلى أحد الأبواب الستة، التي وصفت في كتابي هذا، وقد أتيت على تفسيرها، فأعرف ذلك.
وأنا مخبرك، كيف:
- تضرب الأشياء، وهي الجذور بعضها في بعض، إذا كانت:
- منفردة.
- معها عدد.
- مستثنى منها عدد.
- مستثناة من عدد.
- تجمع بعضها إلى بعض.
- تنقص بعضها من بعض.
إعلم، أنه لابد، لكل عدد يضرب في عدد، من أن يضاعف أحد العددين، بعدد ما في الآخر من الآحاد.
فإذا كانت عقود (الأَعداد: العشَرةُ والعشرون إِلى التسعين)، ومعها آحاد، أو مستثنى منها آحاد، فلابد من ضربها أربع مرات: العقود في العقود، العقود في الآحاد، الآحاد في العقود، والآحاد في الآحاد.
فإذا كانت الآحاد التي مع العقود، زائدة جميعاً، فالضرب الرابع زائد أيضاً.
وإذا كان أحدهما زائداً، والآخر ناقصاً، فالضرب رابع ناقص.
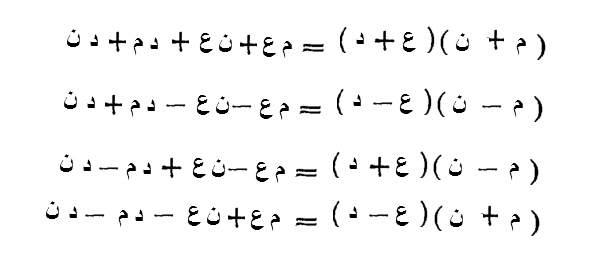
وهو مثل:
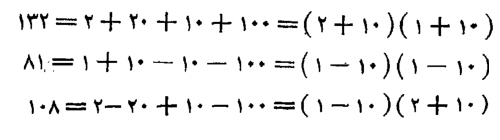
عشرة وواحد، في عشرة واثنين، فالعشرة في العشرة مائة، والواحد في العشرة، عشرة زائدة، والاثنان في العشرة، عشرون زائدة، والواحد في الاثنين، اثنان زائدان، فذلك كله مائة واثنان وثلاثون.
وإذا كانت عشرة إلا واحداً، في عشرة إلا واحداً، فالعشرة في العشرة، مائة، والواحد الناقص في العشرة، عشرة ناقصة، والواحد الناقص أيضاً في العشرة، عشرة ناقصة، فذلك ثمانون، والواحد الناقص، في الواحد الناقص، واحد زائد، فذلك أحد وثمانون.
وإذا كانت عشرة واثنان، في عشرة إلا واحداً، فالعشرة في العشرة مائة، والواحد الناقص في العشرة، عشرة ناقصة، والاثنان الزائدان في العشرة عشرون زائدة، فذلك مائة وعشرة، والاثنان الزائدان في الواحد المنقوص، اثنان ناقصان، فذلك كله مائة وثمانية.
كذلك، لو أنه قال لك، درهم إلا سدساً، في درهم إلا سدساً، يكون، خمسة أسداس في مثلها، وهي خمسة وعشرين جزءاً، من ستة وثلاثين من أجزاء الدرهم، وهو ثلثان وسدس السدس.
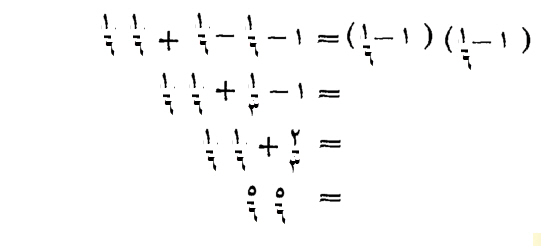
قياسه، أن تضرب درهماً في درهم، فيكون درهماً، و درهم في إلا سدساً بسدس ناقص، وإلا سدساً في درهم بسدس ناقص، فيكون ثلثي درهم، وإلا سدساً في سدس بسدس السدس زائداً، فذلك ثلثان وسدس السدس.
وإنما بينت هذا، لتستدل به على ضرب الأشياء (الجذور ) بعضها في بعض، إذا كان معها عدد، أو استثنيت من عدد، أو استثنى منها عدد.
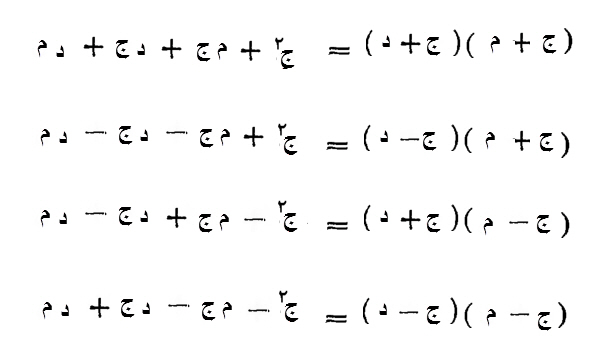
فإذا قيل لك، عشرة إلا شيئاً، ومعنى الشيء الجذر، مضروبة في عشرة، فأضرب عشرة في عشرة، يكون مائة، إلا شيئاً في عشرة يكون عشرة أجذار ناقصة، فتقول، مائة إلا عشرة أشياء.
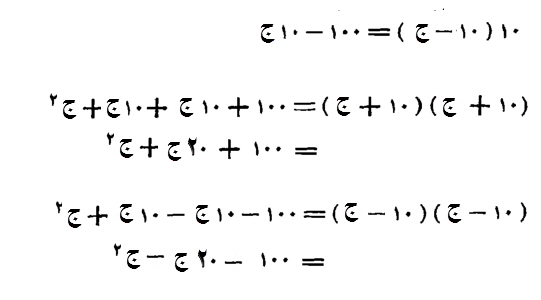
فإن قال عشرة وشيء، في عشرة، فاضرب عشرة في عشرة، يكون مائة، وشيئاً في عشرة يكون عشرة أجذار زائدة، فتقول، مائة وعشرة أشياء.
وان قال، عشرة وشيء، في مثلها، قلت، عشرة في عشرة مائة، وعشرة في شيء عشرة أشياء، وعشرة في شيء بعشرة أشياء أيضاً، وشيء في شيء مال زائد، فيكون ذلك مائة درهم، وعشرين شيئاً، ومالاً زائداً.
وإن قال، عشرة إلا شيئاً، في عشرة إلا شيئاً، قلت، عشرة في عشرة بمائة، وإلا شيئاً في عشرة عشرة أشياء ناقصة، وإلا شيئاً في عشرة عشرة أشياء ناقصة، وإلا شيئاً في إلا شيئاً مال زائد، فيكون ذلك، مائة ومالاً إلا عشرين شيئاً.
وإن قال، عشرة إلا شيئاً، في عشرة وشيء، قلت عشرة في عشرة بمائة، وإلا شيئاً في عشرة عشرة أشياء ناقصة، وشيء في عشرة عشرة أشياء زائدة، وإلا شيئاً في شيء مال ناقص، فيكون لك مائة درهم إلا مالاً.
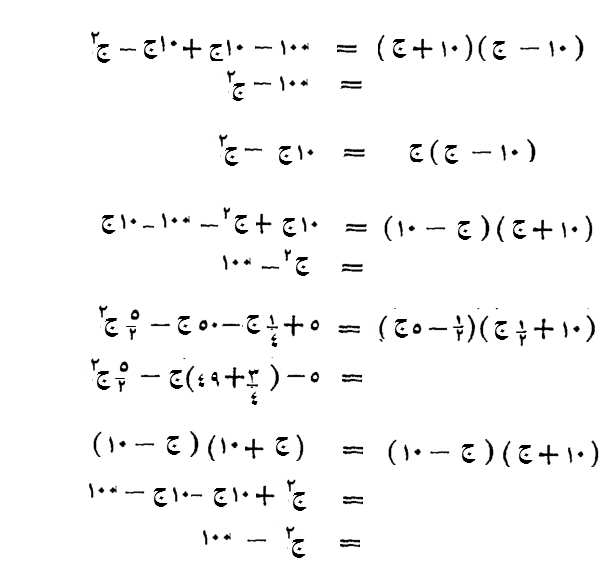
وإن قال، عشرة إلا شيئاً، في شيء، قلت، عشرة في شيء عشرة أشياء، وإلا شيئاً في شيء مال ناقص، فيكون عشرة أشياء إلا مالاً.
وإن قال، عشرة وشيء، في شيء إلا عشرة، قلت شيء في عشرة عشره أشياء زائدة، وشيء في شيء مال زائد، وإلا عشرة في عشرة مائة درهم ناقصة، وإلا عشرة في شيء بعشرة أشياء ناقصة، فتقول، مال إلا مائة درهم، بعد ما قابلت به، وذلك، أن تطرح عشرة أشياء زائدة، بعشرة أشياء ناقصة، فيبقى مال إلا مائة درهم.
وإن قال، عشرة درهم ونصف شيء، في نصف درهم إلا خمسة أشياء، قلت، نصف درهم في عشرة بخمسة دراهم زائدة، ونصف درهم في نصف شيء بربع شيء زائد، وإلا خمسة أشياء في عشرة دراهم خمسون جذراً ناقصة، فيكون جميع ذلك خمسة دراهم إلا تسعة وأربعين جذراً وثلاثة أرباع جذر، ثم تضرب خمسة أجذار ناقصة في نصف جذر زائد فيكون مالين ونصفا ناقصاً، فذلك خمسة دراهم، إلا مالين ونصفا، وإلا تسعة وأربعين جذراً وثلاثة أرباع جذر.
فإن قال، عشرة وشيء، في شيء إلا عشرة، فكأنه قال، شيء وعشرة، في شيء إلا عشرة، فتقول، شيء في شيء مال زائد، وعشرة في شيء عشرة أشياء زائدة، وإلا عشرة في شيء عشرة أشياء ناقصة، فذهبت الزيادة بالنقصان، وبقي المال، وإلا عشرة في عشرة مائة منقوصة من المال، فجميع ذلك مال إلا مائة درهم.
وكل ما كان من الضرب، زائداً وناقصاً، مثل إلا شيئاً، في زيادة شيء، فالضرب الأخير ناقص أبداً، فاعلم ذلك وبالله التوفيق.
إعلم، أن جذر مائتين، إلا عشرة، مجموع، إلى عشرين إلا جذر مائتين، فإنه عشرة سوياً.
وجذر مائتين، إلا عشرة، منقوص من، عشرين إلا جذر مائتين، فهو ثلاثون إلا جذري مائتين، فهو ثلاثون وجذر ثماني مائة.
ومائة، ومال، إلا عشرين جذراً، مجموع إليه، خمسون، وعشرة أجذار، إلا مالين، فهو مائة وخمسون، وإلا مال، وإلا عشرة أجذار.
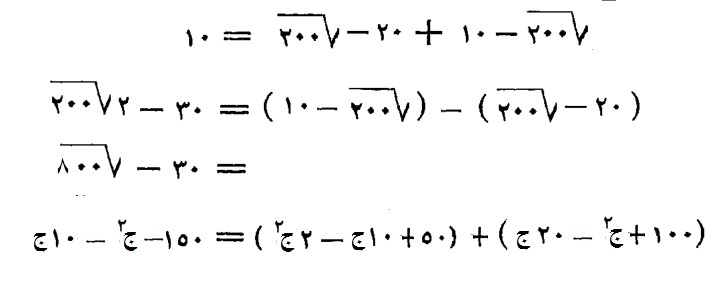
وأنا مبين لك علة ذلك، في صورة، تؤدى إلى الطلب، إن شاء الله تعالى.
واعلم، أن كل جذر مال، معلوم أو أصم، تريد أن تضعفه، ومعنى اضعافك إياه أن تضربه في اثنين، فينبغي، أن تضرب اثنين في اثنين، ثم في المال، فيصير جذر ما اجتمع، مثلي جذر ذلك المال.
وإن أردت ثلاثة أمثاله، فاضرب ثلاثة في ثلاثة، ثم في المال، فيكون جذر ما اجتمع، ثلاثة أمثال جذر ذلك المال الأول.
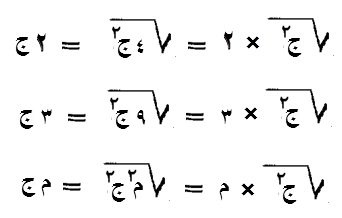
كذلك ما زاد من الأضعاف أو نقص فعلى هذا المثال نفسه.
وإن أردت أن تأخذ نصف جذر مال، فينبغي أن تضرب نصفاً في نصف، فيكون ربعاً، ثم في المال، فيكون جذر ما اجتمع، مثل نصف جذر ذلك المال.
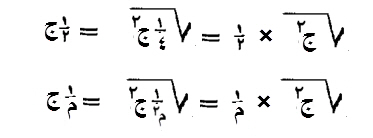
وكذلك، ثلثه أو ربعه، أو أقل من ذلك، أو أكثر، بالغاً ما بلغ في النقصان والأضعاف.
مثال ذلك:
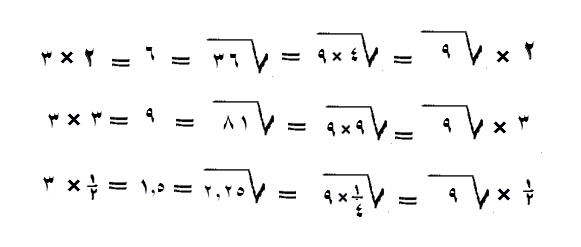
إذا أردت أن تضعف جذر تسعة، ضربت اثنين في اثنين، ثم في تسعة، فيكون ستة وثلاثين، فخذ جذره، يكون ستة، وهو ضعف جذر تسعة.
ولو أردت، أن تضعف جذر تسعة ثلاث مرات، ضربت ثلاثة في ثلاثة ثم في تسعة، فكون أحد وثمانين، فخذ جذره تسعة، وذلك جذر تسعة مضاعفاً ثلاث مرات.
وإن أردت، أن تأخذ نصف جذر تسعة، فإنك تضرب نصفا في نصف، فيكون ربعا، ثم تضرب ربعا في تسعة، فيكون اثنين وربعا. تأخذ جذرها، وهو واحد ونصف، وهو نصف جذر تسعة.
كذلك، ما زاد أو نقص، من المعلوم والأصم، فهذا طريقه.
٩ - قسمة، مربع جذر، على مربع جذر
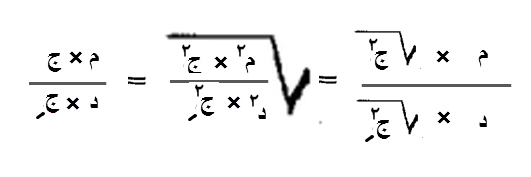
وإن أردت، أن تقسم جذر تسعة، على جذر أربعة، فإنك تقسم، تسعة على أربعة، فيكون اثنين وربعا، فجذرها، هو ما يصيب الواحد، وهو واحد ونصف.
وإن أردت، أن تقسم جذر أربعة، على جذر تسعة، فأنك تقسم أربعة على تسعة، فيكون أربعة أتساع واحد، فجذرها ما يصيب الواحد، وهو ثلثا واحد.
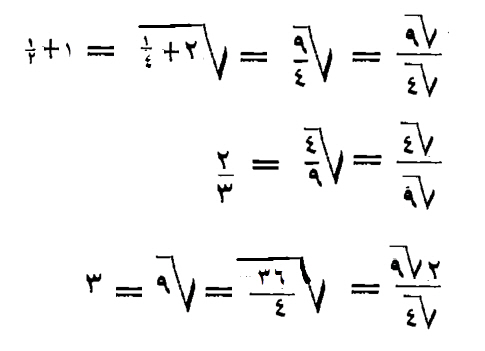
فإن أردت، أن تقسم جذري تسعة، على جذر أربعة، أو غيرها من الأموال، فأضعف جذر التسعة، على ما أرأيتك في عمل الأضعاف، فما بلغ، فاقسمه على أربعة، أو على ما أردت أن تقسم عليه، واعمل به كما عملت.
وإن أردت، ثلاثة أجذار تسعة، أو أكثر، أو نصف جذر تسعة، أو أقل، أو ما كان، فعلى هذا المنوال فاعمله، تصب إن شاء الله تعالى.
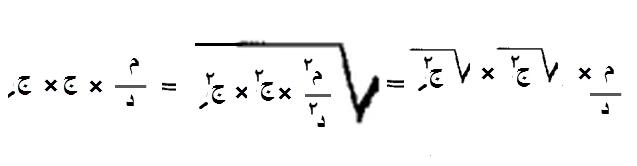
وإن أردت، أن تضرب جذر تسعة، في جذر أربعة، فاضرب، تسعة في أربعة، فيكون ستة وثلاثين، فخذ جذرها وهو ستة، وهو جذر تسعة، مضروب، في جذر أربعة.
ولو أردت أن تضرب جذر خمسة، في جذر عشرة، فاضرب خمسة في عشرة، فجذر ما بلغ، هو الشيء الذي تريده.
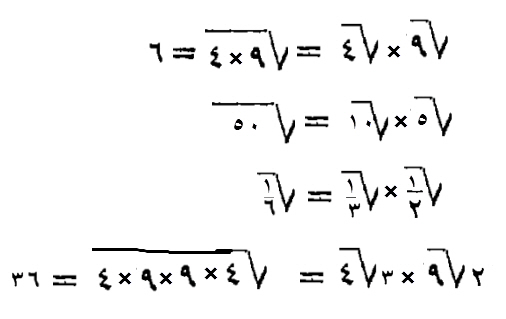
وإن أردت، أن تضرب جذر ثلث، في جذر نصف، فاضرب ثلثا، في نصف، فكون سدسا، فجذر السدس، هو جذر الثلث، مضروب في جذر النصف.
وإن أردت، أن تضرب جذري تسعة، في ثلاثة أجذار أربعة، فاستخرج جذري تسعة، كما وصفت لك، حتى تعلم جذر أي مال هو، وكذلك فافعل، بثلاثة أجذار الأربعة، حتى تعلم جذر أي مال هو، ثم أضرب المالين أحدهما في الآخر، فجذر ما اجتمع لك، هو جذر تسعة، في ثلاثة أجذار أربعة.
وكذلك، كلما زاد من الأجذار، أو نقص، فعلى هذا المثال فاعمل به.
علة، جذر مائتين، إلا عشرة، مجموعا، إلى عشرين، إلا جذر مائتين
صورة ذلك،

خط أ ب، هو جذر مائتين.
خط أ ج، هو العشرة.
خط ج ب، هو جذر مائتين، إلا عشرة.
خط ب د، هو العشرين، وهو مثلاً أ ج.
خط ب ه، هو جذر مائتين، وهو مثل خط أ ب.
خط ه د، هو عشرين، إلا جذر مائتين.
قطعنا خط ز ه، من خط ب ه، مثل خط ج ب.
زدنا على خط ه د، خط ز ه، فتبين لنا، أنه قد نقص من خط ب د، الذي هو عشرون، مثل خط ب ز ، الذي هو عشرة، وهو خط أ ج ، وبقي لنا خط ز د، وهو عشرة.
ذلك ما أردنا أن نبين.
علة، جذر مائتين، إلا عشرة، منقوصاً من، عشرين إلا جذر مائتين
صورة ذلك:
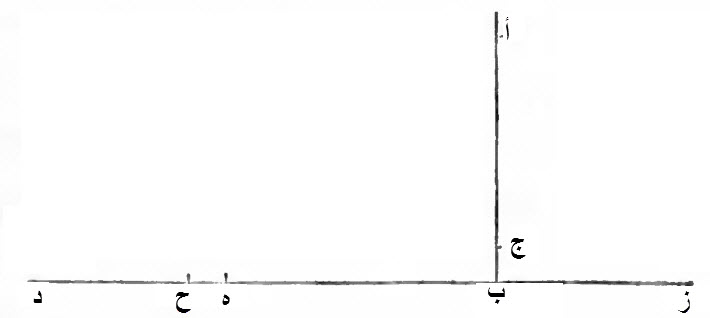
خط أ ب، هو جذر مائتين.
خط أ ج، هو العشرة المعلومة.
خط ج ب، هو ما بقي من جذر مائتين، بعد إلقاء العشرة.
خط ب د، نجعله العشرين.
خط ب ه، نجعله مثل جذر مائتين، وهو مثل خط أ ب.
خط د ه، هو ما بقي من العشرين، بعد إلقاء جذر المائتين.
خط ب ز، نجعله مثل خط أ ج، الذي هو العشرة.
خط ز د، مثل خط ز ب، وخط ب د، ذلك كله ثلاثون.
خط ه ح، نجعله، مثل خط ج ب.
خط ب ز و ه ح هو جذر المأتيين أيضاً .
أردنا، أن ننقص، خط ج ب، من خط ه د، وهو خط ح د.
خط ح د، هو خط ز د، الا، ز ب، و ب ه و ه ح، الذي هو ثلاثون وجذرا مائتين، الذي هو ثلاثون و جذر ثماني مائة.
ذلك ما أردنا أن نبين.
علة، مائة ومال إلا عشرين جذراً، مجموع إليه، خمسون وعشرة أجذار إلا مالين
لم تستقم له صورة، لأنه من ثلاثة أجناس مختلفة، أموال، جذور، وعدد وليس معها ما يعادلها، فتصور، وقد تمكنننا لها صورة لا تحسن.
فأما اضطرارها باللفظ، فبين.
ذلك، إنك قد علمت أن معك مائة، ومالاً، إلا عشرين جذراً، فلما زدت عليها خمسين، وعشرة أجذار، صارت مائة وخمسين، ومالاً، إلا عشرة أجذار.
العشرة الأجذار المزيدة، جبرت من العشرين الجذر الناقصة، عشرة أجذار.
وقد كان مع المائة مال، فلما نقصت من المائة والمال، المالين المستثنيين من الخمسين ذهب، مال بمال، وبقي عليك مال، فصارت مائة وخمسين، إلا مالاً، وإلا عشرة أجذار.
ذلك ما أردنا أن نبين.
و هذه ست مسائل، اقدمها، جعلتها أمثلة، للستة الأبواب، التي ذكرتها في صدر كتابي هذا، وقد أتيت على تفسير هذه الأبواب، واخبرت أن منها ثلاثة ضروب، لا تنصف فيها الأجذار ، وذكرت أن حساب الجبر والمقابلة، لا بد أن يخرجك إلى باب منها.
واتبعت هذه المسائل، بما يقرب من الفهم، وتخفّ فيه المؤنة، وتسهل فيه الدلالة إن شاء اللّه تعالى.
عشرة جزأتها قسمين.
ضربت أحد القسمين في الآخر.
ضربت أحدهما في نفسه.
صار المضروب في نفسه، مثل أحد القسمين في الآخر، أربع مرات.
قياسه:
تجعل أحد القسمين شيئاً، والآخر عشرة إلا شيئاً.
تضرب شيئاً، في عشرة إلا شيئاً، فتكون عشرة أشياء، إلا مالاً.
تضربه في أربعة، لقولك أربع مرات، فيكون أربعة أمثال المضروب من أحد القسمين في الآخر، فيكون ذلك، أربعين شيئاً إلا أربعة أموال.
تضرب شيئاً في شيء، وهو أحد القسمين في نفسه، فيكون، مالاً، يعدل أربعين شيئاً إلا أربعة أموال.
اجبرها بالأربعة الأموال، وزدها على المال، فيكون أربعين شيئاً، تعدل خمسة أموال.
المال الواحد، يعدل ثمانية أجذار، وهو أربعة وستون، جذرها ثمانية، وهو أحد القسمين المضروب في نفسه.
الباقي من العشرة اثنان، وهو القسم الآخر.
وقد أخرجتك هذه المسألة، إلى أحد الأبواب الستة، وهي أموال تعدل جذوراً، فاعلم ذلك.
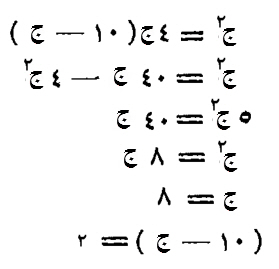
عشرة جزأتها قسمين.
ضربت كل قسم في نفسه، ثم ضربت العشرة في نفسها.
ما اجتمع، من ضرب العشرة في نفسها، مثل أحد القسمين، مضروباً في نفسه مرتين وسبعة أتساع مرة، أو مثل الآخر، مضروباً في نفسه، ست مرات وربع مرة.
قياس ذلك:
تجعل أحد القسمين شيئاً، والآخر عشرة إلا شيئاً.
تضرب الشيء في نفسه، فيكون مالاً، ثم في اثنين وسبعة أتساع، فيكون مالين وسبعة أتساع مال.
تضرب العشرة في مثلها، فيكون مائة.
مائة، تعدل مالين، وسبعة أتساع مال.
أردد إلى مال واحد، وهو تسعة أجزاء من خمسة وعشرون جزءاً، وهو خمس وأربعة أخماس الخمس، فخذ خمس المائة وأربعة أخماس خمسها، وهو ستة وثلاثون، تعدل مالاً.
فخذ جذرها ستة، وهو أحد القسمين، والآخر أربعة لا محالة.
أخرجتك هذه المسألة، إلى أحد الأبواب الستة، وهي أموال تعدل عدداً.
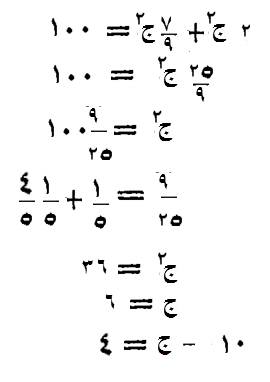
عشرة، جزأتها قسمين.
قسمت أحدهما على الآخر، فخرج القسم أربعة.
قياس ذلك:
تجعل أحد القسمين شيئاً، والآخر عشرة إلا شيئاً.
تقسم عشرة إلا شيئاً، على شيء، ليكون أربعة.
متى ما ضربت، ما خرج لك من القسم، في المقسوم عليه، عاد المال الذي قسمته.
القسم في هذا المسألة أربعة، والمقسوم عليه شيء.
اضرب أربعة في شيء، فيكون أربعة أشياء، تعدل المال الذي قسمته وهو عشرة إلا شيئاً.
اجبر العشرة بالشيء، وزده على الأربعة الأشياء، فيكون خمسة أشياء، تعدل عشرة.
الشيء الواحد اثنان، وهو أحد القسمين.
أخرجتك هذه المسألة، إلى أحد الأبواب الستة، وهي جذور تعدل عدداً.
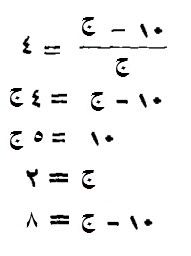
شيء ضربت ثلثه ودرهماً، في ربعه ودرهم، فكان عشرين.
قياسه:
تضرب ثلث شيء، في ربع شيء، فيكون نصف سدس مال.
تضرب درهماً، في ثلث شيء، فيكون ثلث شيء.
تضرب درهماً في ربع شيء، بربع شيء.
تضرب درهماً في درهم، بدرهم.
ذلك كله، نصف سدس مال، وثلث شيء، وربع شيء، ودرهم، يعدل عشرين درهماً.
الق من العشرين درهماً، بدرهم، يبقي، تسعة عشر درهماً، تعدل، نصف سدس مال وثلث شيء وربع شيء.
كمل مالك، وإكماله أن تضرب كل ما معك، في اثني عشر، فيصير معك مال، وسبعة أجذار، تعدل مائتين وثمانية وعشرون درهماً.
فنصف الأجذار، واضربها في مثلها، تكن اثني عشر وربعاً.
زدها على الأعداد، وهي مائتان وثمانية وعشرون، فتكون مائتين وأربعين وربعاً.
خذ جذرها، خمسة عشر ونصفاً، فانقص منه نصف الأجذار، وهو ثلاثة ونصف، يبقى اثنى عشر، وهو المال.
أخرجتك هذه المسألة، إلى أحد الأبواب الستة، وهو أموال وجذور تعدل عدداً.
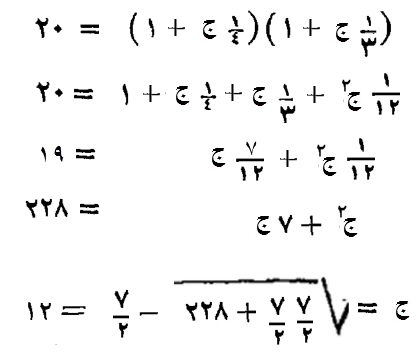
عشرة قسمتها قسمين، ثم ضربت كل قسم في نفسه، وجمعتهما، فكانا ثمانية وخمسين درهماً.
قياسه:
تجعل أحد القسمين شيئاً، والآخر عشرة إلا شيئاً.
اضرب عشرة إلا شيئاً، في مثلها، فيكون، مائة، ومالاً، إلا عشرين شيئاً.
اضرب شيئاً في شيء، فيكون مالاً.
اجمعهما، فيكون ذلك، مائة ومالين إلا عشرين شيئاً، يعدل ثمانية وخمسين درهماً.
اجبر المائة، والمالين، بالعشرين الشيء الناقصة، وزدها على الثمانية والخمسين، فيكون، مائة ومالين، يعدل ثمانية وخمسين درهماً، وعشرين شيئاً.
أردد ذلك إلى مال واحد، وهو أن تأخذ نصف ما معك، فيكون خمسين درهماً ومالاً، يعدل، تسعة وعشرين درهماً وعشرة أشياء.
قابل به، وذلك أنك تلقي من الخمسين، تسعة وعشرين، فيبقي إحدى وعشرون ومال، تعدل عشرة أشياء.
نصف الأجذار تكون خمسة.
اضربها في مثلها، فتكون خمسة وعشرين.
الق منها الواحد والعشرين، التي مع المال، فيبقى أربعة.
خذ جذرها، وهو اثنان، فأنقصه من نصف الأجذار، التي هي خمسة، فيبقى ثلاثة، وهي أحد القسمين، والآخر سبعة.
أخرجتك هذه المسألة إلى أحد الأبواب الستة، وهو أموال وعدد تعدل جذوراً.

شيء ضربت ثلثه في ربعه، فعاد الشيء، وزيادة أربعة وعشرين درهماً.
قياسه:
تضرب ثلث شيء، في ربع شيء فيكون، نصف سدس مال، تعدل شيئاً وأربعة وعشرين درهماً.
تضرب نصف سدس المال في اثني عشر، حتى تكمل مالك، واضرب الشيء في اثني عشر يكن اثني عشر شيئاً، واضرب الأربعة والعشرين في اثني عشر، فيصير معك، مائتان وثمانية وثمانون درهماً واثني عشر جذراً تعدل مالاً.
نصف الأجذار، تكون ستة. اضربها في مثلها، وزدها على مائتين وثمانية وثمانين، فتكون ثلاثمائة وأربعة وعشرين.
خذ جذرها، وهو ثمانية عشر، وزده على نصف الأجذار، وهي ستة.
يكون ذلك أربعة وعشرين، وهو المال.
أخرجتك هذه المسألة، إلى أحد الأبواب الستة، وهي جذور وعدد تعدل أموالاً.
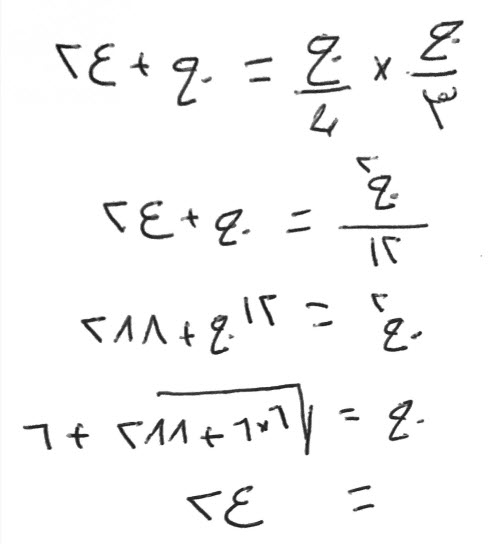
إن سأل سائل ، فقال، عشرة قسمتها قسمين، ثم ضربت أحدهما في الآخر، فكان واحداً وعشرين درهماً.
أحد قسمي العشرة شيء، والآخر عشرة إلا شيئاً.
اضرب شيئاً، في عشرة إلا شيئاً، يكون عشرة أشياء إلا مالاً، يعدل أحداً وعشرين.
اجبر العشرة الأشياء، بالمال، وزده على الواحد والعشرين، فيكون، عشرة أشياء تعدل واحد وعشرين درهماً ومالاً.
إلق نصف الأجذار، فبقي خمسة، اضربها في مثلها تكن خمسة وعشرين.
إلق منها الواحد والعشرين التي مع المال، فتبقى أربعة.
خذ جذرها، وهو اثنان، أنقصه من نصف الأجذار وهي خمسة، يبقى ثلاثة وذلك أحد القسمين.
وإن شئت، زدت جذر الأربعة على نصف الأجذار، فتكون سبعة، وهو أحد القسمين.
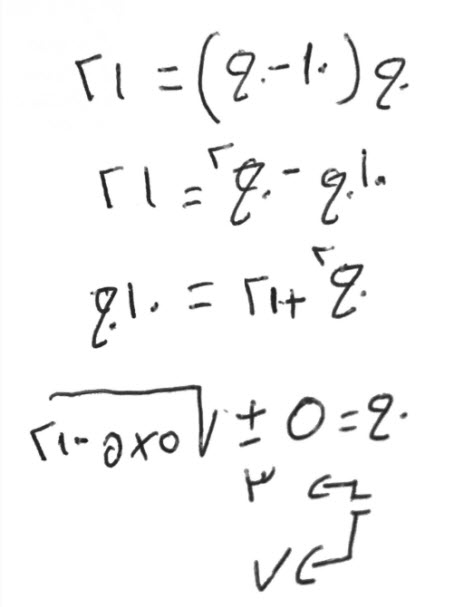
هذه المسألة التي تعمل بالزيادة والنقصان.
وإن قال، عشرة جزأتها قسمين، فضربت كل قسم في نفسه، ثم ألقيت الأقل من الأكثر، فبقي أربعون.
قياسه:
تضرب عشرة إلا شيئاً في مثلها، فتكون مائة ومالاً إلا عشرين شيئاً.
تضرب شيئاً في شيء فيكون مالاً.
انقصه من المائة والمال إلا عشرين شيئاً، تبقى، مائة إلا عشرين شيئاً، تعدل، أربعين درهما.
اجبر المائة، بالعشرين شيئا، وزدها على الأربعين، فيكون، مائة تعدل عشرين شيئاً وأربعين درهماً.
الق الأربعين من المائة، يبقى ستون درهماً تعدل عشرين شيئاً، فالشيء الواحد يعدل ثلاثة، وهو أحد القسمين.
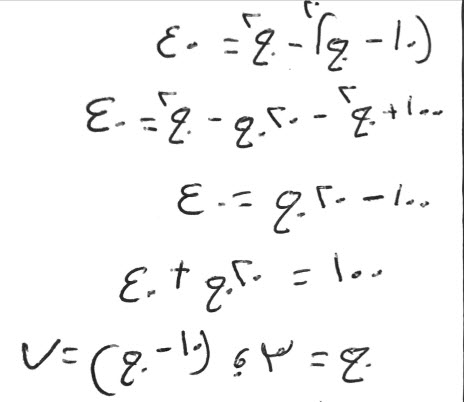
وإن قال، عشرة قسمتها قسمين، فضربت كل قسم في نفسه، وجمعتهما، وزدت عليهما فضل ما بين القسمين من قبل أن تضربهما، فبلغ ذلك أربعة وخمسين درهماً.
قياسه:
تضرب عشرة إلا شيئاً في مثلها، فتكون مائة ومالاً إلا عشرين شيئاً.
تضرب الشيء الباقي من العشرة، في مثله، فيكون مالاً.
تجمع ذلك، فيكون مائة ومالين إلا عشرين شيئاً.
قال، زدت عليهما فضل ما بينهما، قبل ان تضربهما، فقلت، فضل ما بينهما عشرة إلا شيئين.
جميع ذلك، مائة وعشرة ومالان إلا اثنين وعشرين شيئاً، يعدل، أربعة وخمسين درهماً.
فإذا جبرت وقابلت، قلت مائة وعشرة دراهم ومالان، تعدل أربعة وخمسين درهماً واثنين وعشرين شيئاً.
أردد المالين إلى مال واحد، وهو أن تأخذ نصف ما معك، فيكون، خمسة وخمسين درهماً ومالاً، تعدل سبعة وعشرين درهماً وأحد عشر شيئاً.
إلق سبعة وعشرون، من خمسة وخمسين، يبقى، ثمانية وعشرون درهماً ومالا، تعدل أحد عشر شيئاً.
نصف الأشياء، يكون خمسة ونصفاً.
اضربها في مثلها، فيكون ثلاثين وربعاً.
أنقص منها الثمانية والعشرين التي مع المال، يبقي اثنان وربع.
خذ جذرها، وهو واحد ونصف، وأنقصه من نصف الأجذار، يبقى أربعة وهو أحد القسمين.
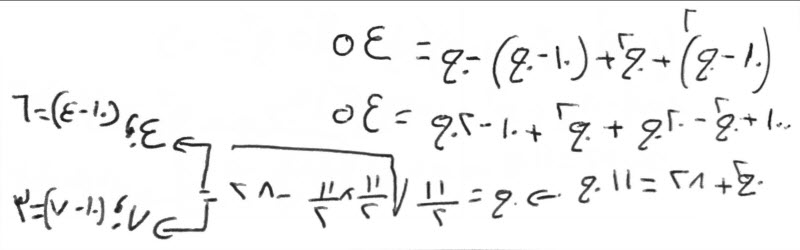
إن قال، عشرة قسمتها قسمين، فقسمت هذا على هذا، وهذا على هذا، فبلغ ذلك درهمين وسدساً.
قياس ذلك:
إذا ضربت كل قسم في نفسه، ثم جمعتهما، كان مثل أحد القسمين إذا ضربت أحداهما في الآخر، ثم ضربت الذي اجتمع معك من الضرب في الذي بلغ القسم، وهو اثنان وسدس.
اضرب عشرة إلا شيئاً في مثلها، تكون مائة ومالاً إلا عشرين شيئاً.
اضرب شيئاً في شيء فيكون مالاً.
اجمع ذلك، يصير مائة ومالين إلا عشرين شيئاً، يعدل، شيئاً مضروباً في عشرة إلا شيئاً، وذلك، عشرة أشياء إلا مالاً، مضروباً في ما خرج من القسمين، وهو اثنان وسدس.
يكون ذلك أحداً وعشرين شيئاً وثلثي شيء إلا مالين وسدساً، تعدل، مائة ومالين إلا عشرين شيئاً.
اجبر ذلك، وزد مالين وسدساً، على مائة ومالين إلا عشرين شيئاً، وزد العشرين الشيء الناقصة من المائة والمالين، على الواحد والعشرين الشيء وثلثي الشيء.
يكون معك، مائة وأربعة أموال وسدس مال، تعدل أحداً وأربعين شيئاً وثلثي شيء.
أردد ذلك إلى مال، وقد علمت أن المال الواحد من أربعة أموال وسدس، هو خمسها وخمس خمسها، فخذ من جميع ما معك، الخمس وخمس الخمس.
يكون معك، أربعة وعشرون ومال، تعدل، عشرة أجذار، لأن، العشرة من أحد وأربعين شيئاً وثلثي شيء، خمسها وخمس خمسها.
نصف الأجذار هي خمسة.
اضربها في مثلها، فتكون خمسة وعشرين.
إنقص منها الأربعة والعشرين التي مع المال، يبقى واحد.
خذ جذره وهو واحد.
أنقصه من نصف الأجذار وهي خمسة.
بقي أربعة وهو أحد القسمين.
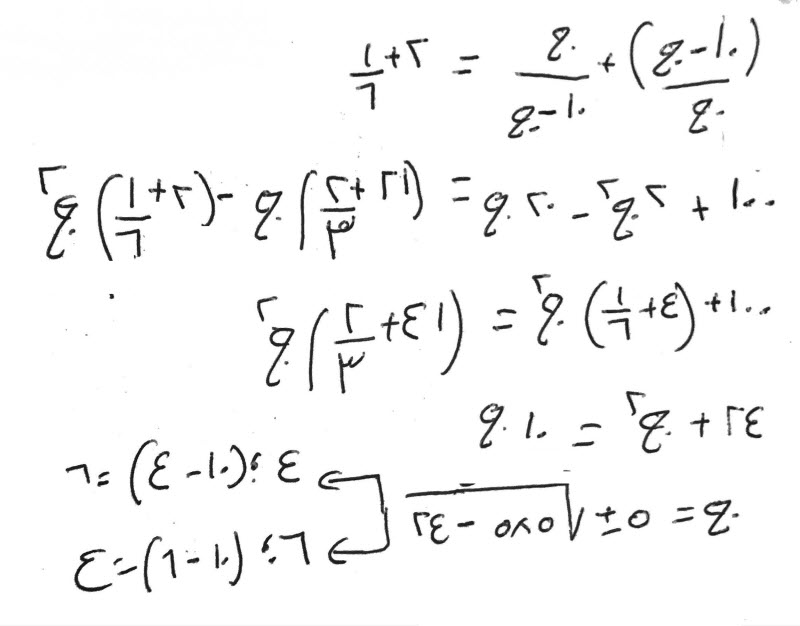
واعلم بأن كل شيئين، تقسم هذا على هذا وهذا على هذا، فإنك إذا ضربت الذي يخرج من هذا في الذي يخرج من هذا، كان واحداً أبداً.
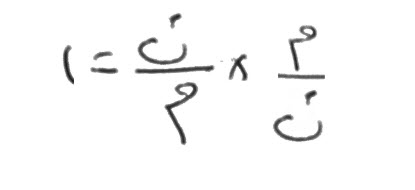
إن قال، عشرة قسمتها قسمين، وضربت أحد القسمين في خمسة، وقسمته على الآخر، ثم ألقيت نصف ما اجتمع معك، وزدته على المضروب في خمسة فكان خمسين درهماً.
قياس ذلك:
تأخذ شيئاً من العشرة، فتضربه في خمسة، فيكون خمسة أشياء، مقسومة على الباقي من العشرة، وهو عشرة إلا شيئاً، مأخوذ نصفها.
و إنك إذا قسمت الخمسة الأشياء على عشرة إلا شيئاً وأخذت نصف ما خرج، كان ذلك كقسمك نصف الخمسة الأشياء على العشرة إلا شيئاً، فإذا أخذت نصف الخمسة الأشياء، صار شيئين ونصفا، وهو الذي تريد أن تقسمه على عشرة إلا شيئاً، يخرج يعدل خمسين إلا خمسة أشياء، لأنه قال تضم إليه أحد القسمين مضروبا في خمسة، فيكون ذلك كله خمسين.
وقد علمت، أنك متى ضربت ما خرج لك من القسم، في المقسوم عليه، عاد المال.
مالك شيئان ونصف، فاضرب عشرة إلا شيئاً، في خمسين إلا خمسة أشياء، فيكون ذلك، خمسمائة درهم وخمسة أموال إلا مائة شيء، تعدل، شيئين ونصفا.
أردد ذلك إلى مال واحد، فيكون ذلك، مائة درهم ومالاً إلا عشرين شيئاً، تعدل، نصف شيء.
اجبر ذلك المائة، وزد العشرين الشيء على نصف الشيء، فيصير معك، مائة درهم ومال، تعدل، عشرين شيئاً ونصف شيء.
فنصف الأشياء، واضربها في مثلها، وانقص منها المائة، وخذ جذر ما بقي، وانقصه من نصف الأجذار وهو عشرة وربع، فيبقى ثمانية وهو أحد القسمين.
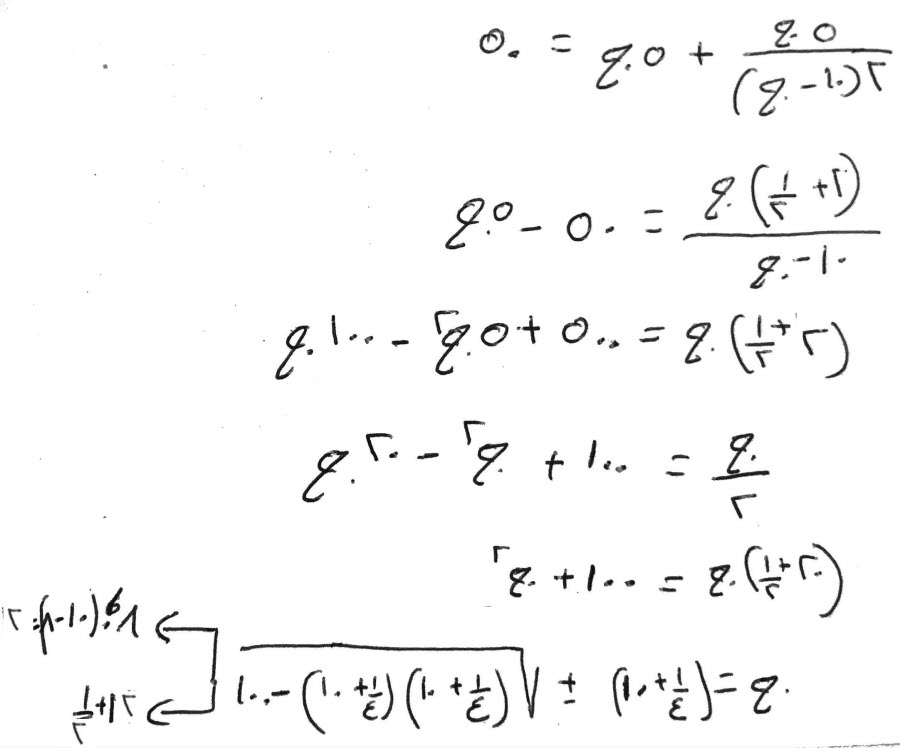
فإن قال، عشرة قسمتها قسمين، فضربت أحد القسمين في نفسه، فكان مثل الآخر إحدى وثمانين مرة.
قياس ذلك:
عشرة إلا شيئاً في مثلها، بمائة ومال إلا عشرين شيئاً، تعدل أحداً وثمانين شيئاً.
اجبر المائة والمال، بالعشرين شيء، وزدها على الواحد والثمانين شيء، فيكون مائة ومالاً، تعدل مائة جذر وجذرا.
فنصف الأجذار تكون خمسين ونصفا، اضربها في مثلها، فيكون ألفين وخمسمائة وخمسين وربعاً.
أنقص منها المائة، يبقى ألفان وأربعمائة وخمسون وربع.
خذ جذرها، وهو تسعة وأربعون ونصف.
أنقصها من نصف الأجذار، وهو خمسون ونصف، فيبقى واحد، وهو أحد القسمين.
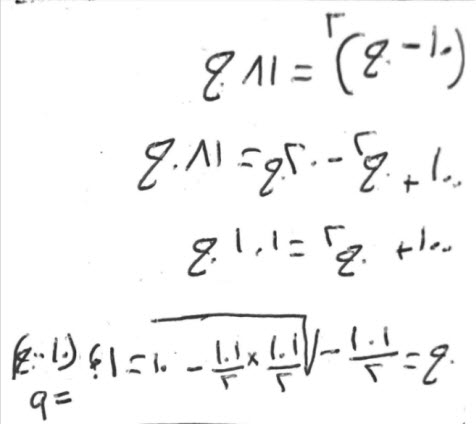
فإن قال، عشرة اقفزة حنطة او شعيراً، بعت كل واحد منهما بسعر، ثم جمعت ثمنهما، فكان ما اجتمع مثل فضل ما بين السعرين، ومثل ما بين الكيلين.
خذ ما شئت فأنه يجوز.
فكأنك أخذت أربعة وستة.
فقلت، بعت كل واحد من الأربعة بشيء، فضربت أربعة في شيء، فصار أربعة أشياء، وبعت الستة، كل واحد، بمثل نصف الشيء الذي بعت به الأربعة، وإن شئت بثلثه، وإن شئت بربعه، وما شئت فأنه يجوز.
فإذا كان بيعك الآخر بنصف شيء، فاضرب نصف شيء في ستة، فيكون ثلاثة أشياء، فأجمعها مع الأربعة الأشياء، فتكون سبعة أشياء، تعدل، ما بين الكيلين وهو قفيزان، وفضل ما بين السعرين وهو نصف شيء، فيكون سبعة أشياء، تعدل اثنين، ونصف شيء.
الق نصف شيء من سبعة أشياء، تبقى، ستة أشياء ونصف شيء، تعدل، درهمين.
الشيء الواحد، أربعة أجزاء من ثلاثة عشر.
تقول، باع الأربعة، كل واحد بأربعة أجزاء من ثلاثة عشر من درهم.
تقول، باع الستة، كل واحد بجزأين من ثلاثة عشر من درهم.
بلغ ذلك، ثمانية وعشرين جزءاً، من ثلاثة عشر من درهم.
ذلك مثل فضل، ما بين الكيلين، وهو قفيزان، فصرفهما ستة وعشرون جزءاً، وفضل ما بين السعرين، وهو جزاءان، فذلك ثمانية وعشرون جزءاً.
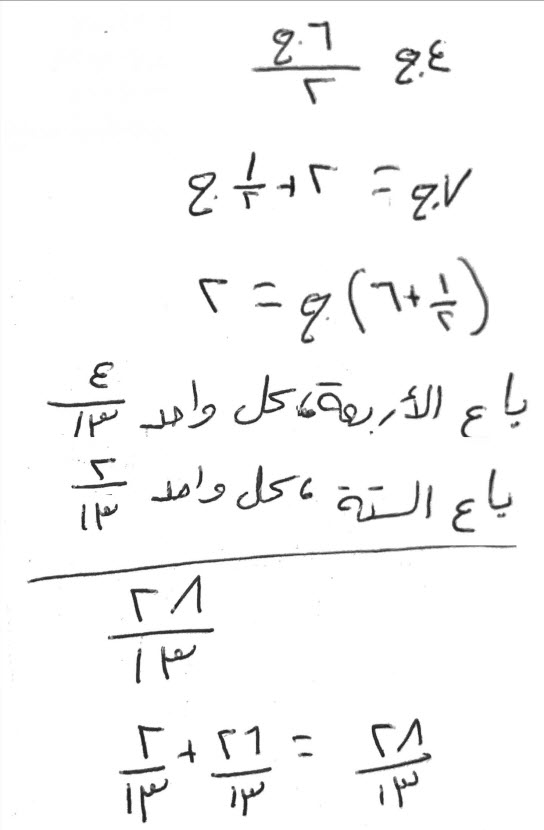
فإن قال، مالان بينهما درهمان، قسمت القليل على الكثير، فأصاب القسم، نصف درهم.
اجعل أحد المالين شيئاً، والآخر شيئاً ودرهمين.
لما قسمت شيئاً على شيء ودرهمين، خرج القسم نصف درهم.
متى ضربت ما خرج لك من القسم، في المقسوم عليه، عاد الذي قسمته، وهو شيء.
شيء ودرهمان، في النصف الذي هو القسم.
نصف شيء ودرهماً تعدل شيئاً.
ألقيت نصف شيء بنصف شيء، وبقي درهم يعدل نصف شيء.
أضعفه، يكون الشيء يعدل درهمين، والآخر أربعة.
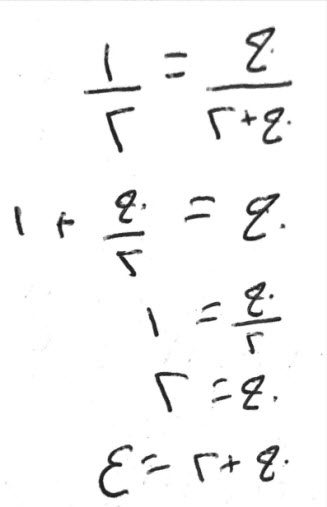
فإن قال، عشرة قسمتها قسمين، وضربت أحدهما في عشرة، والقسم الآخر في نفسه، فاستويا.
قياسه:
تضرب شيئاً في عشرة، فيكون عشرة أشياء.
تضرب عشرة إلا شيئاً في مثلها، فتكون، مائة ومالاً إلا عشرين شيئاً، تعدل العشرة الأجذار.
قابل بها على ما قد وصفت لك.
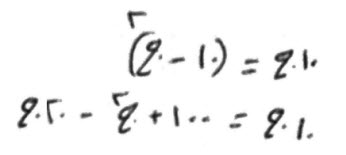
كذلك لو قال، عشرة قسمتها قسمين، ثم ضربت أحدهما في الآخر، ثم قسمت ما اجتمع من الضرب، على فضل ما بين القسمين قبل أن تضرب أحدهما في الآخر، فخرج خمسة وربعاً.
قياسه:
تأخذ شيئاً من العشرة، فيبقى عشرة إلا شيئاً، فاضرب أحدهما في الآخر، فيكون عشرة أجذار إلا مالاً، فهو ما خرج، من ضرب أحد القسمين في الآخر.
قسمت ذلك على فضل ما بين القسمين، وهو عشرة إلا شيئين، فخرج من القسم، خمسة وربع.
متى ضربت خمسة وربعاً، في عشرة إلا شيئين، خرج لك المال المضروب، وهو عشرة أشياء إلا مالاً.
اضرب خمسة وربعاً، في عشرة إلا شيئين، يكون ذلك، اثنين وخمسين درهماً ونصفاً إلا عشرة أجذار ونصفاً، تعدل، عشرة أجذار إلا مالاً.
اجبر الاثنين والخمسين والنصف، بالعشرة الأجذار والنصف، وزدها على العشرة الأجذار إلا مالاً، ثم اجبرها بالمال، وزد المال على اثنين وخمسين درهماً ونصف.
يكون معك، عشرون جذراً ونصف جذر، تعدل اثنين وخمسين درهماً ونصفاً، ومالاً، فقابل بها على ما فسرنا في أول الكتاب.
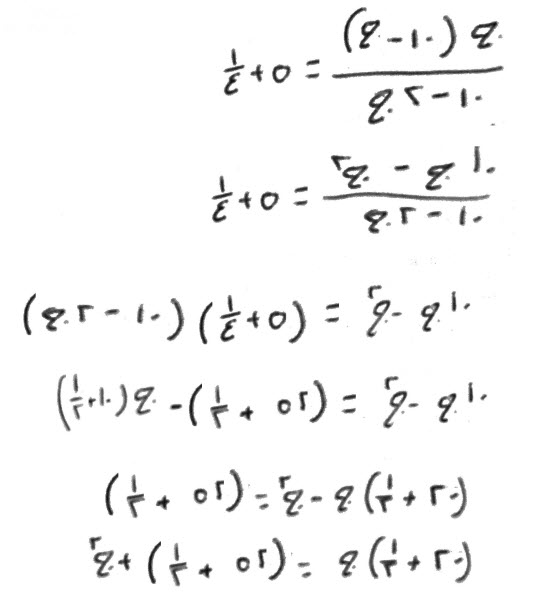
فإن قال، مالا، ثلثا خمسه مثل سبع جذره.
فإن المال كله، يعدل جذراً ونصف سبع جذر، فالجذر، أربعة عشر جزءاً، من خمسة عشر من المال.
قياسه:
تضرب ثلثي خمس مال، في سبعة ونصف، ليتم المال.
أضرب ما معك، وهو سبع جذر، في مثل ذلك، فيصير المال يعدل، جذراً ونصف سبع جذر.
يصير جذره، واحدا ونصف سبع.
فالمال، واحد و، تسعة وعشرون جزءاً من مائة وستة وتسعين من درهم، وثلثا خمسه يكون، ثلاثين جزءاً من مائة وستة وتسعين، وسبع جذره أيضاً، ثلاثون جزءاً من مائة وستة وتسعين.
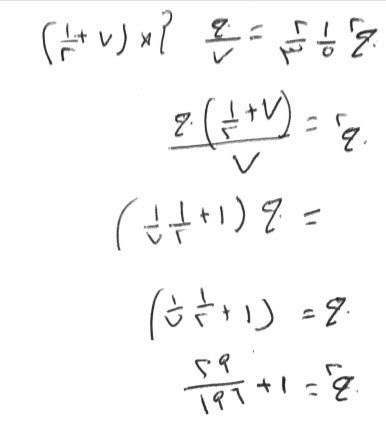
فإن قال، مال ثلاثة أرباع خمسه، مثل أربعة اخماس جذره.
قياسه:
تزيد على ثلاثة أرباع خمسه، مثل ربعها، ليكون الجذر تاماً، وذلك ثلاثة وثلاثة أرباع من عشرين، فاجعلها أرباعاً كلها، فتكون خمسة عشر من ثمانين، فاقسم الثمانين على الخمسة عشر فيكون خمسة وثلاثاً، فذلك جذر المال، والمال ثمانية وعشرون وأربعة أتساع.
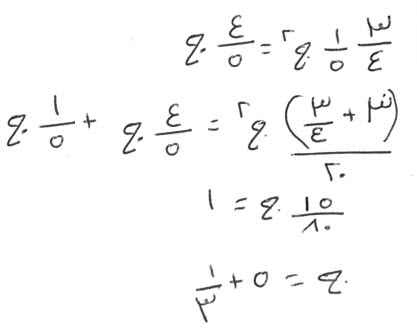
إن قال، مال تضربه في أربعة أمثاله، فيكون عشرين.
قياسه:
أنك إذا ضربته في مثله، كان خمسة، وهو جذر خمسة.
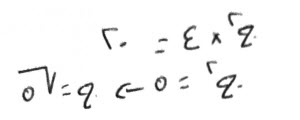
فإن قال، شيء تضربه في ثلثه، فيكون عشرة.
قياسه:
أنك إذا ضربته في مثله، كان ثلاثين، فتقول الشيء هو جذر الثلاثين.
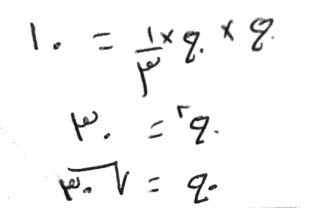
إن قال، شيء تضربه في أربعة أمثاله، يعود ثلث الشيء الأول.
قياسه:
إذا ضربت الشيء في أثني عشر مثله، عاد الشيء، وهو نصف نصف الثلث.

فإن قال، مال تضربه في جذره، فيعود ثلاثة أمثال، المال الأول.
قياسه:
إذا ضربت الجذر، في ثلث المال، عاد المال، فتقول، هذا مال ثلثه جذره، وهو تسعة.
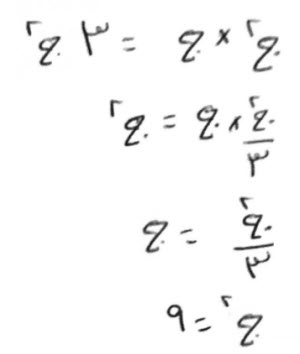
فإن قال، مال تضرب أربعة أجذاره، في ثلاثة أجذاره، فيعود المال وزيادة أربعة وأربعين درهماً.
فقياسه:
تضرب، أربعة أجذار في ثلاثة أجذار، فيكون، اثني عشر مالاً، تعدل، مالاً وأربعة واربعين درهماً.
الق، من الاثني عشر المال، مالاً بمال، فيبقى أحد عشر مالاً، تعدل، أربعة وأربعين درهماً.
اقسمها عليها، تكن أربعة، وهو المال.

فإن قال، مال، تضرب أربعة أجذاره، في خمسة أجذاره، فيعود مثلي المال، وزيادة ستة وثلاثين درهماً.
قياسه:
تضرب أربعة أجذار، في خمسة أجذار، فيكون، عشرين مالاً، تعدل، مالين وستة وثلاثين درهماً.
تلقى من العشرين المال، مالين بمالين، فتبقى، ثمانية عشر مالاً، تعدل، ستة وثلاثين درهماً.
تقسم ستة وثلاثين درهماً، على ثمانية عشر، فيكون القسم اثنين، وهو المال.
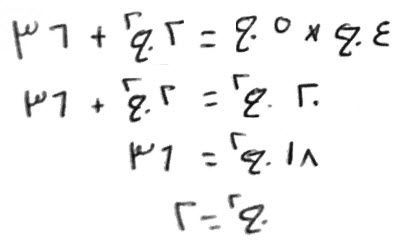
كذلك لو قال، مال تضرب جذره، في أربعة أجذاره، فيعود ثلاثة أمثال المال، وزيادة خمسين درهماً.
قياسه:
تضرب جذراً، في أربعة أجذار، فيكون، أربعة أموال، تعدل، ثلاثة أموال وخمسين درهماً.
الق ثلاثة أموال، من الأربعة الأموال، يبقى، مال واحد، يعدل، خمسين درهماً.
وهو جذر خمسين، مضروب في أربعة أجذار خمسين، أيضاً فذلك مائتان، يكون ثلاثة أمثال المال، وزيادة خمسين، درهماً.
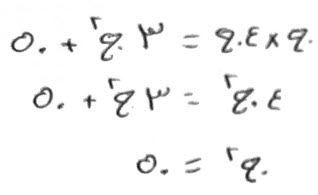
فإن قال، مال تزيد عليه عشرين درهماً، فيكون مثل اثني عشر جذره۔
قياسه:
تقول، مال وعشرون درهماً، تعدل اثني عشر جذراً.
فنصف الأجذار، واضربها في مثلها، تكن ستة وثلاثين.
انقص منها العشرين درهم، وخذ جذر ما بقي.
أنقصه من نصف الأجذار، وهو ستة، فما بقي، فهو جذر المال، وهو درهمان، والمال أربعة.
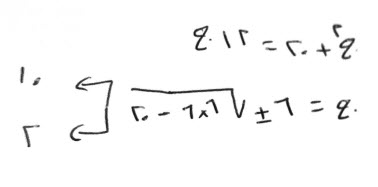
فإن قال، شيء تعزل ثلثه وثلاثة دراهم، وتضرب ما بقي في مثله، فيعود الشيء.
قياسه:
إذا ألقيت، ثلثه وثلاثة دراهم، بقي ثلثاه إلا ثلاثة دراهم.
اضرب ثلثي شيء إلا ثلاثة دراهم، في مثله، فنقول، ثلثان في ثلثين أربعة أتساع مال، وإلا ثلاثة دراهم في ثلثي شيء جذران، وإلا ثلاثة دراهم في ثلثي شيء جذران، وإلا ثلاثة دراهم في إلا ثلاثة دراهم تسعة دراهم، فيصير معك، أربعة أتساع مال، وتسعة دراهم، إلا أربعة أجذار، تعدل، جذرا.
رد الأربعة أجذار، على الجذر، فيكون، خمسة أجذار، تعدل، أربعة أتساع مال وتسعة دراهم.
أكمل مالك، وهو أن تضرب الأربعة أتساع، في اثنين وربع، فيكون مالاً، واضرب تسعة دراهم في اثنين وربع، يكن عشرين وربعاً، ثم اضرب الخمسة الأجذار في اثنين وربع، فيكون أحد عشر شيئاً وربعاً.
يصير معك، مال وعشرون درهما وربع، تعدل، أحد عشر جذراً وربعاً.
قابل بذلك، كنحو ما وصفت لك في تنصيف الأجذار، إن شاء الله.
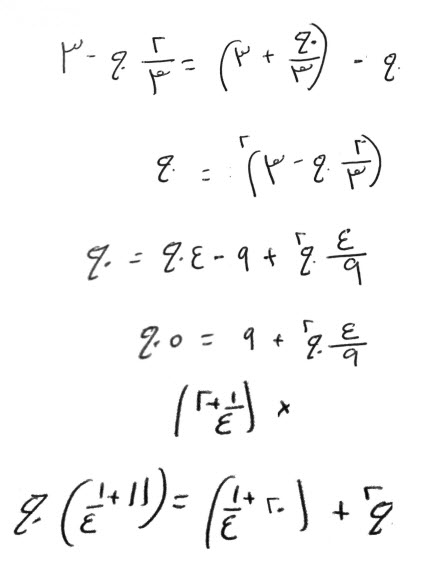
فإن قال، شيء، تضرب ثلثه في ربعه، فيعود الشيء.
قياسه:
تضرب، ثلث شيء في ربع شيء، فيكون نصف سدس مال، تعدل، شيئاً.
المال، يعدل اثني عشر شيئاً، وهو مائة وأربعة وأربعين.
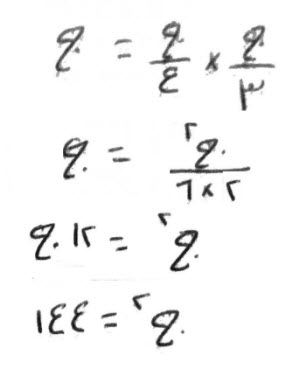
فإن قال، شيء تضرب ثلثه ودرهماً، في ربعه ودرهمين، فيعود الشيء وزيادة ثلاثة عشر درهماً.
قياسه:
تضرب ثلث شيء في ربع شيء فيكون نصف سدس مال، وتضرب درهمين في ثلث شيء فيكون ثلثي جذر، ودرهماً في ربع شيء فيكون ربع جذر، ودرهمين في درهم بدرهمين.
فذلك، نصف سدس مال ودرهمان وأحد عشر جزءاً من اثني عشر جزءاً من جذر، تعدل، جذراً وثلاثة عشر درهماً.
الق درهمين، من ثلاثة عشر بدرهمين، فيبقى أحد عشر درهماً.
الق أحد عشر جزءاً من جذر، فيبقى، نصف سدس جذر وأحد عشر درهماً، تعدل، نصف سدس مال.
أكمل المال، وذلك أن تضربه في اثني عشر، وتضرب كل ما معك في اثني عشر، فيكون، مالاً، يعدل، مائة واثنين وثلاثين درهماً وجذراً.
قابل به، يصب إن شاء الله تعالى، بما وصفت لك.
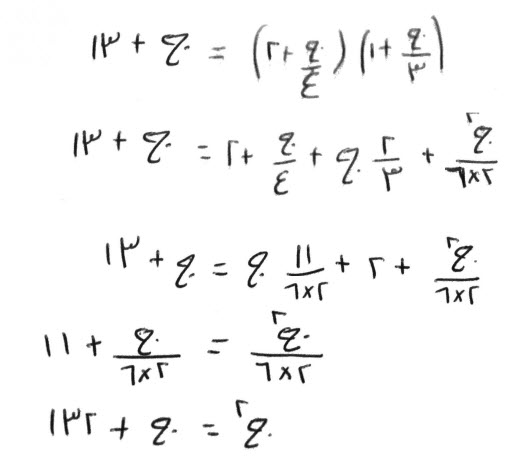
فإن قال، درهم ونصف، مقسوم على رجل وبعض رجل، فأصاب مثلي البعض.
قياسه:
تقول، الرجل والبعض هو واحد وشيء، فكأنه قال، درهم ونصف بين واحد وشيء، فأصاب الواحد شيئين.
اضرب الشيئين، في الواحد والشيء، فيكون، مالين وشيئين، تعدل، درهماً ونصفاً.
ردهما إلى مال واحد، وهو أن تأخذ من كل ما معك نصفه، فتقول، مال وشيء تعدل ثلاثة أرباع درهم.
قابل به، على نحو ما وصفت لك في صدر الكتاب.
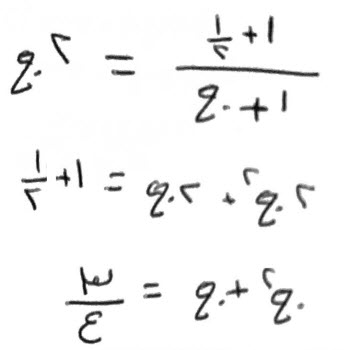
فإن قال، شيء، عزلت ثلثه وربعه وأربعة دراهم، وضربت ما بقي، في مثله، فعاد الشيء، وزيادة اثني عشر درهماً.
قياسه:
تأخذ شيئاً، تعزل ثلثه وربعه، تبقى خمسة أجزاء من أثنى عشر جزءاً من شيء.
تعزل منها أربعة دارهم، فتبقي خمسة أجزاء من إثني عشر جزءاً من شيء، إلا أربعة دراهم.
تضربها في مثلها، فتكون:
الأجزاء الخمسة، خمسة وعشرين جزءاً، وتضرب الاثني عشر في مثلها، فتكون، مائة وأربعة وأربعين، فذلك خمسة وعشرون، من مائة وأربعة وأربعين، من مال.
تضرب الأربعة الدراهم، في الخمسة الأجزاء من اثني عشر من شيء، مرتين، فيكون أربعين جزءاً كل اثني عشر منها شيء.
والأربعة الدراهم في الأربعة الدراهم، ستة عشر درهماً زائدة.
تصير الأربعون جزء، ثلاثة أجذار وثلث جذر، ناقصة.
تحصل معك، خمسة وعشرون جزءاً من مائة وأربعة وأربعين جزءاً من مال، وستة عشر درهماً، إلا ثلاثة أجذار وثلث جذر، تعدل، شيء واثني عشر درهماً.
اجبره، وزد الثلاثة الأجذار والثلث، على الشيء والاثني عشر درهماً، فتصير، أربعة أجذار وثلث جذر واثني عشر درهماً.
قابل به، والق اثني عشر، من ستة عشر، يبقى، أربعة دراهم وخمسة وعشرون جزءا من مائة وأربعة وأربعين من مال، تعدل، أربعة أجذار وثلثا.
يحتاج أن تكمل مالك، واكمالك إياه، أن تضرب جميع ما معك، في خمسة، وتسعة عشر جزءاً، من أجزاء خمسة وعشرين.
تضرب خمسة وعشرين، في خمسة وتسعة عشر جزءاً من خمسة وعشرين، فيكون مالاً.
تضرب الأربعة الدراهم، في خمسة وتسعة عشر جزءاً من خمسة وعشرين، فيكون، ثلاثة وعشرين درهماً، وجزءاً من خمسة وعشرين.
تضرب أربعة أجذار وثلثاً، في خمسة وتسعة جزءاً من خمسة وعشرين، فيكون، أربعة وعشرين جذراً، وأربعة وعشرين جزءأ من خمسة وعشرين، من جذر.
فنصف الأجذار، فيكون اثني عشر جذرا، وأثنى عشر جزءا، من خمسة وعشرين، من جذر.
إضربها في مثلها، يكون، مائة وخمسة وخمسين، وأربعمائة وتسعة وستين جزءاً، من ستمائة وخمسة وعشرين.
الق منها الثلاثة والعشرين، والجزء من الخمسة والعشرين، الذي كان مع المال.
يبقى، مائة واثنان وثلاثون، وأربعمائة وأربعون جزءاً، من ستمائة وخمسة وعشرين.
تأخذ جذر ذلك، وهو إحدى عشر، وثلاثة عشر جزءاً من خمسة وعشرين.
تزيده على نصف الأجذار، التي هي اثني عشر و، اثني عشر جزءاً من خمسة وعشرين.
يكون ذلك أربعة وعشرين.
وهو الشيء المطلوب، الذي تعزل ثلثه، وربعه، وأربعة دراهم، ثم تضرب ما بقي في مثله، فيعود الشيء وزيادة اثني عشر درهماً.
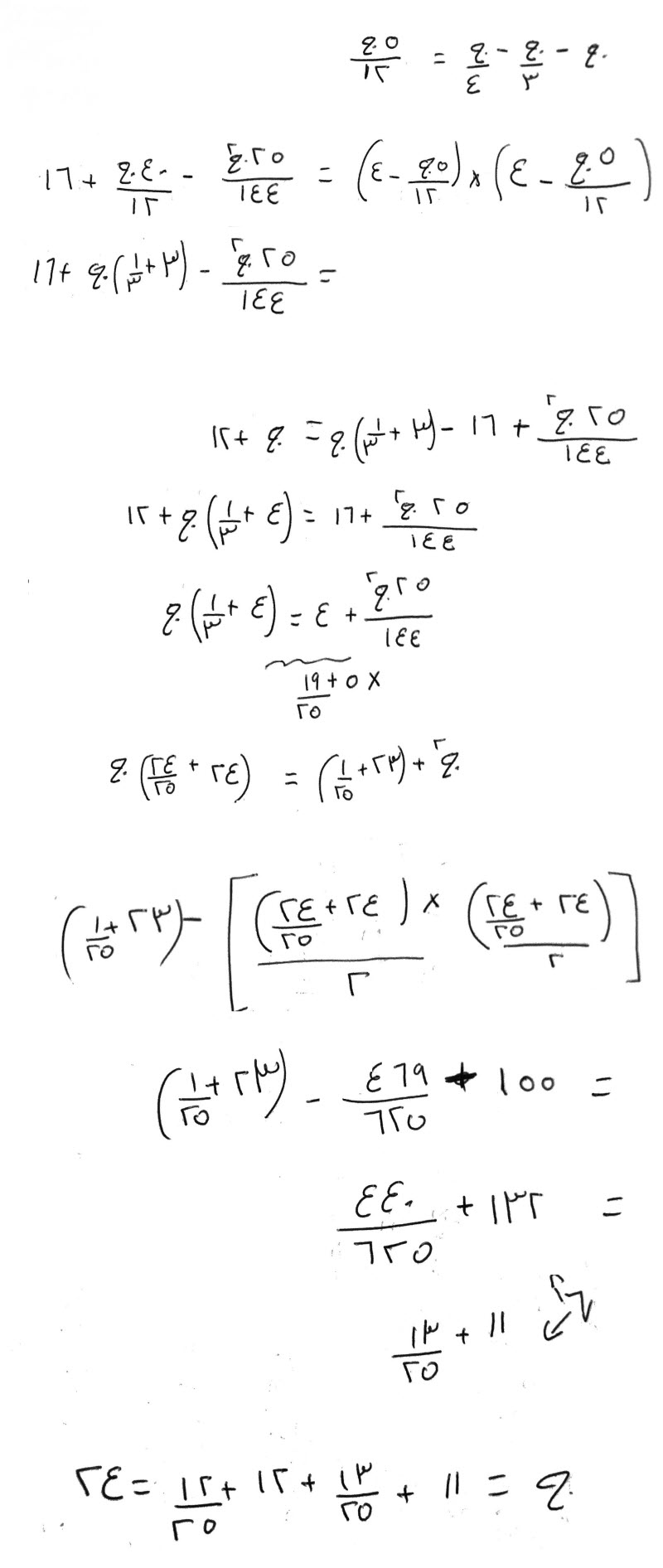
فإن قال، شيء في ثلثيه، فبلغ خمسة.
قياسه:
تضرب شيئًا، في ثلثي شيء، فيكون ثلثي مال، تعدل، خمسة.
أكمله بمثل نصفه، وزد على الخمسة مثل نصفها، يصير معك، مال، يعدل، سبعة ونصفاً.
خذ جذرها، وهو الشيء، الذي تريد أن تضربه في ثلثيه، فيكون خمسة.
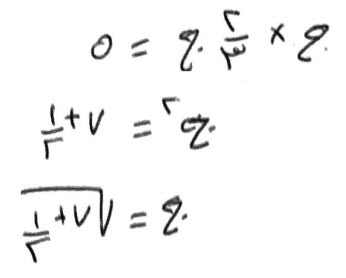
فإن قال، شيئين، بينهما درهمان، قسمت القليل على الكثير، فأصاب القسم، نصف درهم.
قياسه:
تضرب، شيئاً ودرهمين في القسم، وهو نصف، فيكون، نصف شيء ودرهما، تعدل، شيئاً.
ألق، نصف شيء بنصف شيء، يبقى، درهم يعدل نصف شيء.
أضعفه، فيكون معك شيء، يعدل درهمين، وهو أحد الشيئين، والشيء الآخر أربعة.
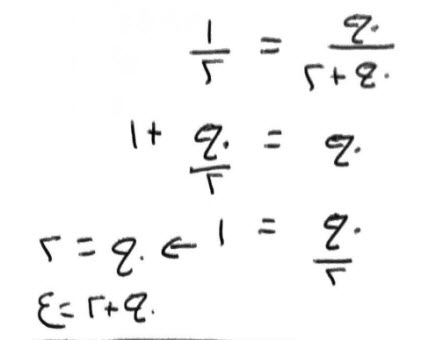
فإن قال، قسمت درهما على رجال، فأصابهم شيء، ثم زدت فيهم رجلا، ثم قسمت عليهم درهما، فأصابهم أقل من القسم الأول، بسدس درهم.
قياسه:
أضرب عدد الرجال الأولين، وهو شيء، في السدس الذي بينهم، فيكون سدس جذر.
اضرب ذلك، في عدد الرجال الأولين والآخرين، وهو، شيء وواحد، يكون، سدس مال، وسدس جذر، مقسوم على درهم تعدل درهما.
كمل المال الذي معك، وهو أن تضربه في ستة، يكون معك مال وجذر.
اضرب الدرهم في ستة، فيكون ستة دراهم.
يكون مالاً وجذراً تعدل ستة دراهم.
فنصف الجذر، واضربه في مثله، فيكون ربعاً.
زده على الستة، وخذ جذر ما اجتمع.
أنقص منه نصف الجذر، الذي كنت ضربته في مثله، وهو نصف.
ما بقي، فهو عدد الرجال الأولين، وهما في هذه المسألة رجلان.
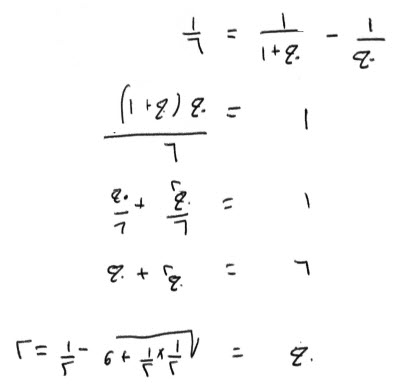
فإن قال، مال تضربه في ثلاثة أجذاره، فيكون خمسة أمثال، المال الأول.
فكأنه قال، مال ضربته في جذره، فكان مثل المال الأول، وثلثيه.
جذر المال، درهم وثلثان.
المال، درهمان وسبعة أتساع.
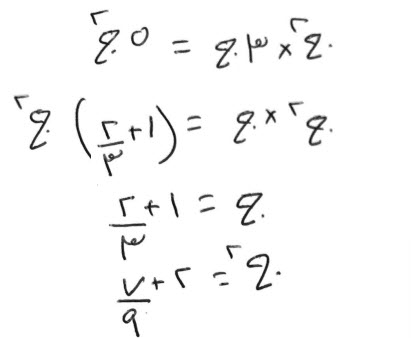
فإن قال، مال تلقي ثلثه، ثم تضرب الباقي، في ثلاثة أجذار المال، فيعود المال الأول.
قياسه:
إذا ضربت المال الأول كله، من قبل أن تلقي ثلثه، في ثلاثة أجذاره، كان مالاً ونصفاً، لأن ثلثيه في ثلاثة أجذاره، مال، فهو كله في ثلاثة أجذاره، مال ونصف، وهو كله في جذر واحد، نصف مال.
فجذر المال نصف، والمال ربع، فثلثا المال سدس، وثلاثة أجذار المال، درهم ونصف.
متى ما ضربت سدساً، في درهم ونصف، خرج ربعاً، وهو المال.
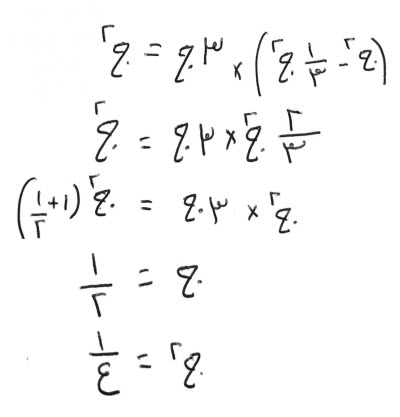
فإن قال ، مال تعزل أربعة أجذاره، ثم تأخذ، ثلث ما بقي، فيكون، مثل الأربعة الأجذار.
قياسه:
ثلث ما بقي، مثل الأربعة أجذار.
ما بقي، مثل اثني عشر جذرا.
زد عليها الأربعة الأجذار، تكون ستة عشر جذراً.
فالمال مائتان وستة وخمسون.
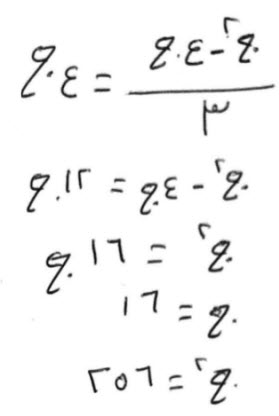
فإن قال، مال عزلت جذره، وزدت على جذره، جذر ما بقي، فكان درهمين.
قياسه:
جذر مال، وجذر، مال إلا جذراً، تعدل درهمين.
الق منه جذر مال، والق من الدرهمين جذر مال، فيكون درهمين إلا جذراً.
في مثله، أربعة دراهم، ومالاً، إلا أربعة أجذار، تعدل، مالاً إلا جذراً.
قابل به، فيكون، مالاً وأربعة دراهم، تعدل مالاً وثلاثة أجذار.
تلقي مالاً بمال، فيبقى ثلاثة أجذار، تعدل، أربعة دراهم.
الجذر، يعدل درهماً وثلثاً، وهو جذر المال، والمال، درهم، وسبعة أتساع درهم.
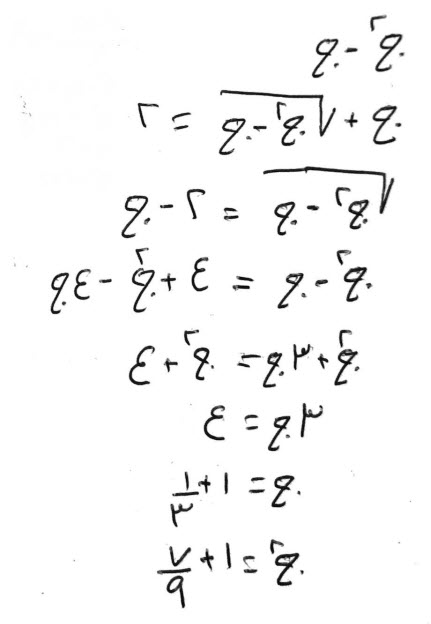
فإن قال، مال تعزل ثلاثة أجذاره، ثم تضرب ما بقي في مثله، فيعود المال.
قياسه:
الذي بقي، هو جذر أيضاً، والمال أربعة أجذار، وهو ستة عشر.
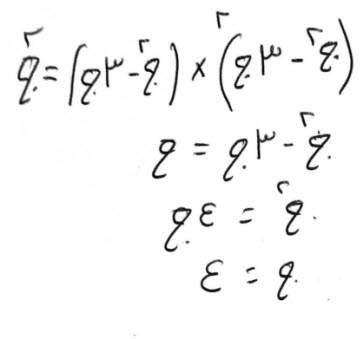
١٤ - باب المعاملات - الأربعة المتناسبة
إعلم، أن معاملات الناس كلها، فمن البيع، والشراء، والصرف، والإجارة، وغير ذلك، على وجهين، بأربعة أعداد يلفظ بها السائل، وهي المُسَعَّرْ، والسِعْرْ، والثَمَنْ، والمُثَمَّنْ.
العدد الذي هو المُسَعَّرْ، مباين للعدد الذي هو والثَمَنْ.
العدد الذي هو السِعْرْ، مباين للعدد الذي هو المُثَمَّنْ.
وهذه الأربعة أعداد ، ثلاثة منها، أبدا ظاهرة معلومة، وواحد منها مجهول، وهو، الذي في قول القائل، كم، وعنه، يسأل السائل.
القياس في ذلك :
تنظر إلى الثلاثة الأعداد الظاهرة، فلا بد أن يكون منها اثنان، كل واحد منهما، مباين لصاحبه.
تضرب، العددين الظاهرين المتباينين، كل واحد منهما في صاحبه.
ما بلغ، فاقسمه على العدد الآخر الظاهر، الذي متباينه مجهول، فما خرج لك، فهو العدد المجهول، الذي يسأل عنه السائل، وهو مباين للعدد الذي قسمت عليه.
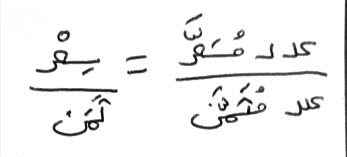
مثال ذلك، في وجه منه:
إذا قيل لك، عشرة بستة، كم لك بأربعة؟
فقوله عشرة، هو العدد المسعر، وقوله بستة، هو السعر، وقوله كم لك؟ هو العدد المجهول المثمن. وقوله بأربعة، هو العدد الذي هو الثمن.
فالعدد المسعر، الذي هو العشرة، مباين للعدد الذي هو الثمن، وهو الأربعة، فاضرب العشرة الأربعة، وهما المتباينان الظاهران، فيكون أربعين.
اقسمها على العدد الآخر الظاهر، الذي هو السعر، وهو ستة، فيكون ستة وثلثين.
وهو العدد المجهول، الذي هو في قول القائل، كم؟ وهو المثمن، ومباينه الستة، الذي هو السعر.

والوجه الثاني:
قول القائل، عشرة بثمانية، كم ثمن أربعة؟ وربما قال، أربعة منها كم ثمنها؟
العشرة هي العدد المسعر، وهو مباين، للعدد، الذي هو الثمن المجهول، الذي في قوله كم.
الثمانية، هي العدد الذي هو السعر، وهو مباين، للعدد الظاهر، الذي هو المثمن، وهو أربعة.
اضرب العددين الظاهرين المتباينين، أحدهما في الآخر، وهو أربعة في ثمانية، فيكون اثنين وثلاثين.
اقسمه، على العدد الآخر الظاهر، الذي هو المسعر، وهو عشرة، فيكون، ثلاثة وخمساً.
هذا هو العدد، الذي هو المثمن، وهو مباين للعشرة، التي عليها قسمت.
هذا هو العدد، الذي هو المثمن، وهو مباين للعشرة، التي عليها قسمت.
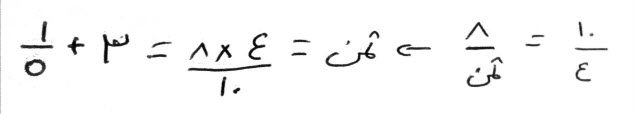
فإن سأل سائل، فقال، أجير أجرته في الشهر عشرة دراهم، عمل ستة أيام، كم نصيبه؟
الستة الأيام هي خمس الشهر.
الذي يصيبه من الدراهم، بقدر ما عمل من الشهر.
قياس ذلك:
شهر، وهو ثلاثون يوماً، وهو المسعر.
عشرة دراهم هو السعر.
ستة أيام هو المثمن.
كم يصيبه هو الثمن.
اضرب السعر، الذي هو عشرة، في المثمن الذي هو مباينه، وهو ستة، فيكون ستين.
اقسمه على الثلاثين، التي هي العدد الظاهر وهو المسعر، فيكون ذلك، درهمين وهو الثمن.
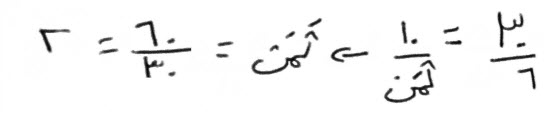
وهذا ما يتعامل الناس به بينهم من الصرف والكيل والوزن.
إعلم، أن معنى واحد في واحد، إنما هي مساحة، ومعناه ذراع في ذراع.
كل سطح، متساوي الأضلاع والزوايا، يكون من كل جانب واحد، فأن السطح كله واحد.
إن كان من كل جانب اثنان، وهو متساوي الأضلاع والزوايا، فالسطح كله أربعة، أمثال السطح الذي هو ذراع في ذراع.
كذلك، ثلاثة في ثلاثة، وما زاد على ذلك أو نقص، وكذلك نصف في نصف، ربع وغير ذلك من الكسور، فعلى هذا.
كل سطح مربع، يكون من كل جانب، نصف ذراع، فهو مثل ربع السطح، الذي هو من كل جانب، ذراع.
كذلك، ثلث في ثلث، وربع في ربع، وخمس في خمس، وثلثان في نصف، أو أقل من ذلك أو أكثر، فعلى حسابه.
وكل سطح مربع، متساوي الأضلاع، فإن أحد أضلاعه في واحد، جذره، وفي اثنين جذراه، صغر هذا السطح أو كبر.
كل مثلث، متساوي الأضلاع،فإن ضربك عمود (الارتفاع)، ونصف القاعدة التي يقع عليها العمود، هو مساحة ذلك المثلث.
وكل مُعيّن (شكل رباعي، أضلاعه الأربعة، متساوية)، متساوي الأضلاع، فان ضربك، أحد القطرين (القطعة المستقيمة، الواصلة بين رأسين غير متتاليين)، في نصف الآخر، هو مساحته.

وكل دائرة، فإن ضربك القطر، في ثلاثة وسبع، هو الدور( محيط)، الذي يحيط بها.
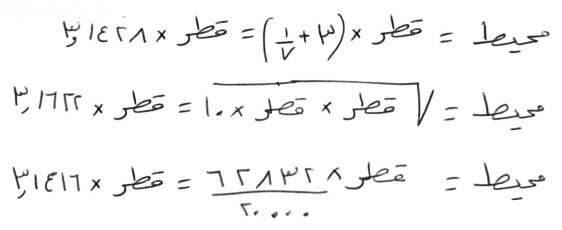
وهو اصطلاح بين الناس من غير اضطرار، ولأهل الهندسة فيه قولان آخران.
أحدهما، أن تضرب القطر، في مثله، ثم في عشرة، ثم تأخذ جذر ما اجتمع، فما كان، هو الدور.
الثاني، لأهل النجوم منهم، وهو، أن تضرب القطر، في اثنين وستين ألفاً وثمانمائة واثنين وثلاثين، ثم تقسم ذلك على، عشرين ألفاً، فما خرج، فهو الدور.
كل ذلك، قريب بعضه من بعض.
والدور، إذا قسمته على ثلاثة وسبع، يخرج القطر.
وكل دائرة، فإن نصف القطر، في نصف الدور، هو مساحتها، لأن، كل ذات أضلاع وزوايا متساوية، من المثلثات، والمربعات، والخمسات، وما فوق ذلك، فإن ضربك، نصف ما يحيط به، في، نصف قطر، أوسع دائرة يقع فيها مساحتها.
وكل دائرة، فإن قطرها مضروباً في نفسه، منقوصا من الحاصل سِبْعَهُ ونصف سِبْعَهُ، هو مساحاتها، وهو موافق للذي ذكر قبل.
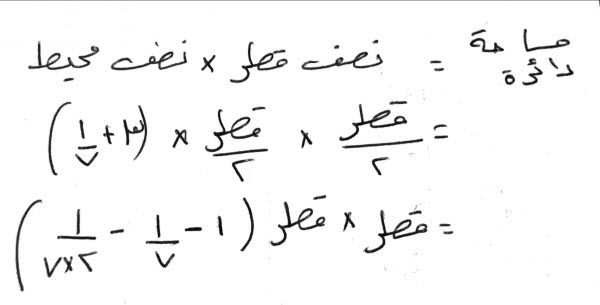
وكل قطعة من دائرة، مشبهة بقوس، فلا بد أن تكون، مثل نصف دائرة، أو أقل من نصف دائرة، أو أكثر من نصف دائرة .
الدليل على ذلك، أن سهم القوس (قطعة مستقيمة تصل بين منتصف قوسٍ ومنتصف وتره)، إذا كان مثل نصف الوتر(قطعة مستقيمة واصلةٌ بين نقطتين على الدائرة )، فهي نصف مدورة سوياً.
وإذا كان السهم، أكثر من نصف الوتر، فهي أكثر، من نصف مدورة.
وإذا أردت أن تعرف من أي دائرة هي، فاضرب نصف الوتر في مثله، اقسمه على السهم، وزد ما خرج، على السهم، فما بلغ، فهو قطر الدائرة التي تلك القوس منها.
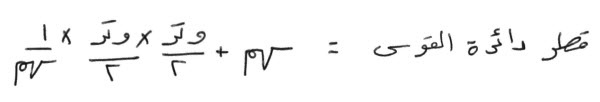
فإن أردت أن تعرف مساحة القوس ، ف:
اضرب، نصف قطر الدائرة، في نصف القوس، واحفظ ما خرج.
أنقص، سهم القوس، من نصف قطر الدائرة، إن كانت القوس، أقل من نصف الدائرة.
إن كانت أكثر من نصف الدائرة، أنقص نصف قطر الدائرة، من سهم القوس.
اضرب ما بقي، في نصف وتر القوس.
انقصه، مما حفظت، إن كانت القوس، أقل من نصف دائرة.
زده على ما حفظت، إن كانت القوس، أكثر من نصف دائرة.
ما بلغ، بعد الزيادة أو النقصان، فهو مساحة القوس.
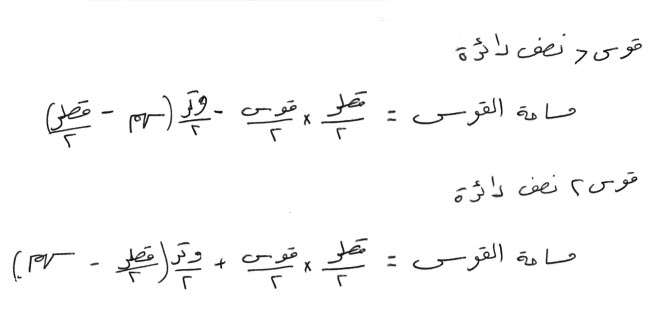
كل مجسم مربع، فإن ضربك الطول، في العرض، في العمق، هو التكسير (المساحة).
إن كان على غير تربيع ، فكان مدوراً، أو مثلثاً، أو غير ذلك، إلا أن عمقه على الاستواء والموازاة، فإن مساحة ذلك، أن تمسح سطحه، فتعرف مساحته، فما كان، ضربته في العمق، وهي المساحة.
وأمّا المخروط، والهرم الثلاثي والهرم المربع، فإن الذي يكون من ضرب ثلث مساحة أسفله، في عموده، هو مساحته.
كل مثلث، قائم الزاوية، فإن الذي يكون، من ضرب الضلعين الاقصرين، كل واحد منهما في نفسه، مجموعين، مثل الذي يكون، من ضرب الضلع الأطول في نفسه.
برهان ذلك:
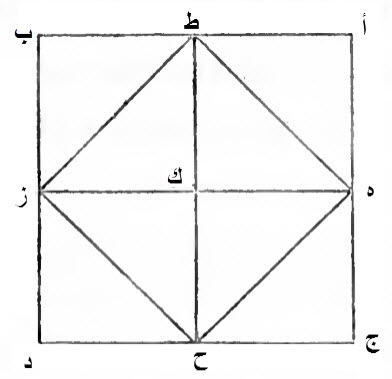
نجعل سطحاً مربعاً، متساوي الأضلاع والزوايا، أ ب ج د.
نقطع ضلع أ ج، بنصفين، على نقطة ه، نخرجه إلى ز.
نقطع ضلع أ ب، بنصفين، على نقطة ط، ونخرجه إلى نقطة ح
صار سطح، أ ب ج د، أربعة سطوح، متساوية الأضلاع والزوايا والمساحة، وهي أ ك، ج ك، ب ك ،و د ك.
نخرج، من نقطة ه، إلى نقطة ط، خطاً، يقطع سطح أ ك نصفين.
حدث من السطح، مثلثان، وهما مثلثا، أ ط ه ، و ه ك ط.
أ ط نصف أ ب، أ ه مثله، وهو نصف أ ج.
وترهما خط ط ه، على زاوية قائمة۔
كذلك، نخرج خطوطاً من ط إلى ز، ومن ز إلى ح، ومن ح إلى ه.
حدث، من جميع المربعات، ثمانية مثلثات متساويات.
أربع منها، نصف السطح الأعظم، الذي هو أ د.
خط أ ط، في نفسه، مساحة مثلثين.
خط أ ه، في نفسه، مساحة مثلثين مثلهما.
يكون جميع ذلك، مساحة أربع مثلثات.
ضلع ه ط، في نفسه، أيضاً مساحة أربع مثلثات أخر.
الذي يكون من ضرب أ ط في نفسه، أ ه في نفسه، مجموعين، مثل الذي يكون من ضرب ط ه في نفسه.
ذلك ما أردنا أن نبين، وهذه صورته.
إعلم، أن المربعات خمسة أجناس ، فمنها:
- مستوية الأضلاع، قائمة الزوايا.
- قائمة الزوايا، مختلفة الأضلاع، طولها، أكثر من عرضها.
- المعينة، وهي، التي استوت اضلاعها، واختلفت زواياها.
- المشبهة بالمعينة، وهي، التي طولها وعرضها مختلفان، وزواياها مختلفة، غير أن، الطولين متساويان، والعرضين متساويان.
- المختلفة الأضلاع والزوايا.
فما كان من المربعات، المستوية الأضلاع، قائمة الزوايا ، أو، المختلفة الأضلاع، القائمة الزوايا، فإن مساحتها، أن تضرب الطول في العرض، فما بلغ فهو التكسير (المساحة).
مثال ذلك، أرض مربعة، من كل جانب خمسة أذرع، مساحتها خمسة وعشرون ذراعاً، وهذه صورتها.
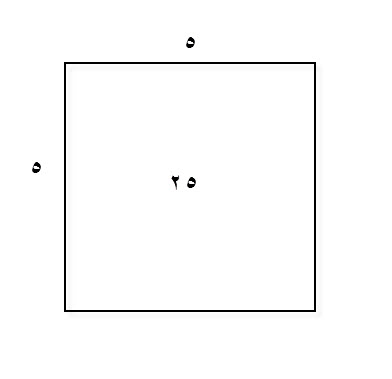
الجنس الثاني، أرض مربعة، طولها، ثمانية أذرع، ثمانية أذرع، والعرضان، ستة، ستة.
مساحتها، تضرب ستة في ثمانية، فيكون ثمانية وأربعين ذراعاً، وذلك تكسيرها وهذه صورتها.
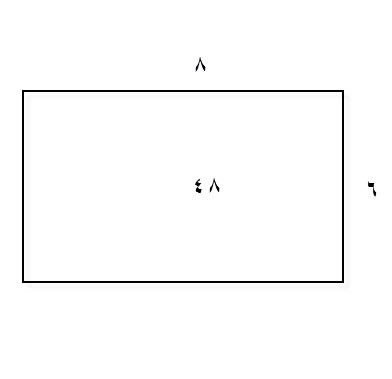
أمّا المعينة، المستوية الأضلاع، التي كل جانب منها، خمسة أذرع، وأحد قطريها ثمانية، والآخر ستة أذرع، فأعلم، أن مساحتها، أن تعرف القطرين، أو أحدهما.
إن عرفت القطرين جميعاً، فإن الذي يكون، من ضرب أحدهما في نصف الآخر، هو تكسيرها.
ذلك، أن تضرب ثمانية في ثلاثة، أو أربعة في ستة، فيكون أربعة وعشرون ذراعاً، وهو مساحتها.
فإن عرفت قطراً واحداً، فقد علمت، أنهما مثلثان، كل واحد منهما، ضلعاه، خمسة أذرع، خمسة أذرع، والضلع الثالث هو قطرهما.
احسبهما على حساب المثلثات وهذه صورتها.
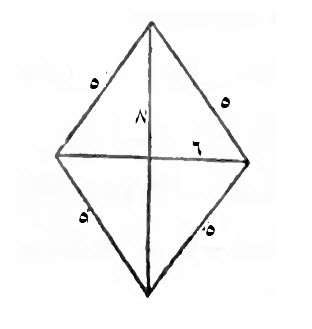
أمّا المشبهة بالمعينة، فعلى مثال المعينة، وهذه صورة المشبه بالمعينة.

أمّا سائر المربعات، فإنما تعرف مساحتها، من قبل القطر، فيخرج إلى حساب المثلثات، فاعلم ذلك.
وأمّا المثلثات، فهي ثلاثة أجناس ، القائمة، الحادة، والمنفرجة.
أمّا القائمة، فهو مثلث، إذا ضربت ضلعيه الأقصرين، كل واحد منهما في نفسه، ثم جمعتهما، كان ذلك، مثل ضلعه الأطول، في نفسه.
أمّا الحادة، فكل مثلث، إذا ضربت ضلعيه الأقصرين، كل واحد منهما في نفسه، ثم جمعتهما، كانا أكثر، من الضلع الأطول، مضرباً في نفسه.
أمّا المنفرجة، فهو كل مثلث، إذا ضربت ضلعيه الأقصرين، كل واحد منهما في نفسه، وجمعتهما، كانا أقل، من الضلع الأطول، مضروباً في نفسه.
أمّا القائمة الزوايا، فهي التي لها عمودان، وقطر، وهي نصف مربعة. معرفة مساحتها، أن تضرب، أحد الضلعين المحيطين بالزاوية القائمة، في نصف الآخر، فما بلغ ذلك فهو مساحتها.
مثل ذلك، مثلث قائم الزاوية، ضلع منه ستة أذرع، وضلع منه ثمانية أذرع، والقطر عشرة.
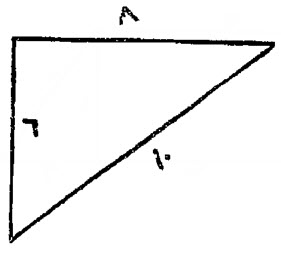
حساب ذلك، تضرب ستة في أربعة، فيكون أربعة وعشرين ذراعاً، وهو مساحتها.
وإن أحببت أن تحسبها بالعمود، فإن عمودها، لا يقع إلا على الضلع الأطول، لأن الضلعين القصيرين عمودان. فإن أردت ذلك، فاضرب عمودها في نصف القاعدة، فما كان، فهو مساحتها.
أمّا الجنس الثاني، فالمثلث، المتساوي الأضلاع، حاد الزوايا . من كل جانب عشرة أذرع.
إن مساحته، تعرف من قبل عموده، ومسقط حجره.
واعلم، أن كل ضلعين مستويين من مثلث، يخرج بينهما عمود على قاعدة، فإن مسقط حجر العمود، يقع على زاوية قائمة، ويقع على نصف القاعدة سواء، إذا استوى الضلعان.
فإن اختلفا، خالف مسقط الحجر، عن نصف القاعدة.
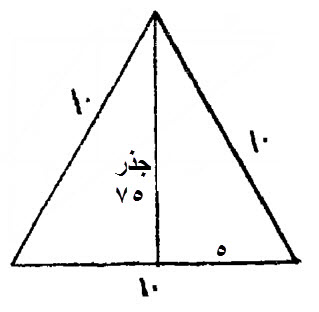
وقد علمنا، أن مسقط حجر هذا المثلث، على أي أضلاعه، جعلته لا يقع إلا على نصفه، فذلك خمسة أذرع.
معرفة العمود، أن تضرب الخمسة في مثلها، وتضرب أحد الضلعين في مثله، وهو عشرة فيكون مائة، فتنقص منها مبلغ الخمسة في مثلها وهو خمسة وعشرون، فيبقى خمسة وسبعون.
خذ جذر ذلك، فهو العمود، قد صار ضلعا، على مثلثين قائمين.
فإن أردت المساحة، فأضرب جذر الخمسة والسبعين، في نصف القاعدة، وهو خمسة.
ذلك، أن تضرب الخمسة في مثلها، حتى يكون جذر خمسة وسبعون، في جذر خمسة وعشرين، فأضرب خمسة وسبعين، في خمسة وعشرين، فيكون ألفاً وثماني مائة وخمسة وسبعين.
خذ جذر ذلك، وهو مساحة المثلث، وهو ثلاثة وأربعون، وشيء قليل.
وقد تكون، من هذه الزوايا الحادة، مختلفة الأضلاع، فاعلم، أن مساحتها، تعلم من قبل مسقط حجرها، وعمودها.
وهي، أن تكون مثلثة، من جانب خمسة عشر ذراعاً، ومن جانب أربعة عشر ذراعاً، ومن جانب ثلاثة عشر ذراعاً.
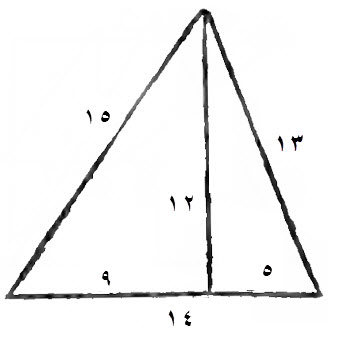
فإذا أردت علم مسقط حجرها، فاجعل القاعدة أي الجوانب شئت، فجعلناها أربعة عشر، وهو مسقط الحجر.
مسقط حجرها، يقع منها على شيء، مما يلي أي الضلعين شئت، فجعلنا الشيء مما يلي الثلاثة عشر.
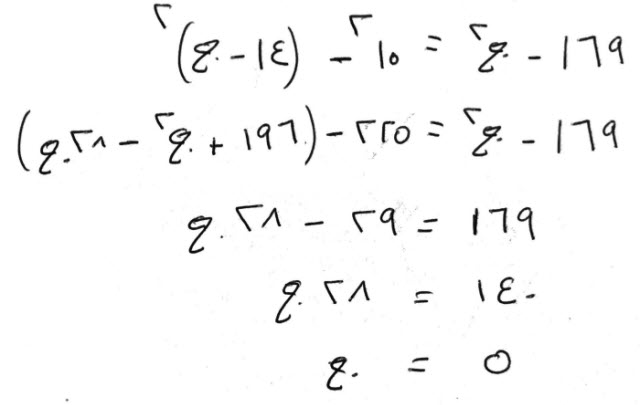
ضربناه في مثله، فصار مالاً، ونقصناه من ثلاثة عشر، في مثلها، وهو مائة وتسعة وستون.
صار ذلك، مائة وتسعة وستين، إلا مالاً.
علمنا أن جذرها هو العمود.
بقي لنا من القاعدة، أربعة عشر إلا شيئاً.
ضربناه في مثله، فصار، مائة وستة وتسعين، ومالاً، إلا ثمانية وعشرن شيئاً.
نقصناه من الخمسة عشر في مثلها، فبقي تسعة وعشرون، وثمانية وعشرون شيئاً، إلا مالاً، وجذرها هو العمود.
لما صار جذرها هذا، هو العمود، وجذر مائة وتسعة وستين، إلا مالاً، هو العمود أيضاً، علمنا أنهما متساويان.
قابل بينهما، وهو، أن تلقي مالاً بمال، لأن المالين ناقصان، فيبقى، تسعة وعشرون وثمانية وعشرون شيئاً، تعدل، مائة وتسعة وستين.
ألق، تسعة وعشرين من مائة، وتسعة وستين، فيبقى، مائة وأربعون، تعدل، ثمانية وعشرين شيئاً.
الشيء الواحد خمسة، وهو مسقط الحجر مما يلي الثلاثة عشر، وتمام القاعدة مما يلي الضلع الآخر، فهو تسعة.
إذا أردت أن تعرف العمود، اضرب هذه الخمسة في مثلها، وأنقصها من الضلع الذي يليها، مضروباً في مثله، وهو ثلاثة عشر.
يبقى مائة وأربعة وأربعون، وجذر ذلك هو العمود، وهو اثني عشر.
العمود، ابدا يقع على القاعدة، على زاويتين قائمتين، ولذلك سمى عموداً، لأنه مستو.
اضرب العمود، في نصف القاعدة وهو سبعة، فيكون أربعة وثمانين، وذلك مساحة المثلث.
والجنس الثالث، المنفرجة، وهي التي لها زاوية منفرجة، وهي مثلثة من كل جانب، عدد مختلف.
وهي، من جانب ستة، ومن جانب خمسة، ومن جانب تسعة.
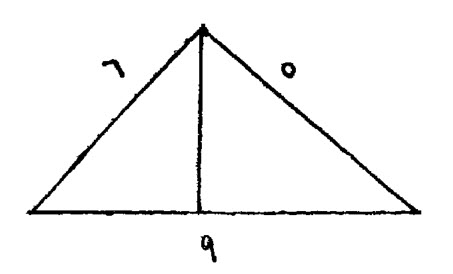
معرفة مساحة هذه، من قبل عمودها، ومسقط حجرها، ولا يقع مسقط هذه المثلثة في جوفها، إلا على الضلع الأطول، فاجعله قاعدة.
لو جعلت أحد الضلعين الأقصرين قاعدة، لوقع مسقط حجرها، خارجها.
علم مسقط حجرها وعمودها، على مثال ما عملت لك في الحادة، وعلى ذلك القياس.
أمّا الدائرات، التي فرغنا من صفتها، ومساحتها، في صدر الكتاب، فمنها، دائرة قطرها سبعة أذرع، فمحيطها اثنان وعشرون ذراعاً.
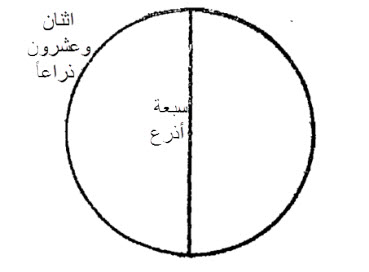
مساحتها، أن تضرب نصف القطر، وهو ثلاثة ونصف، في نصف الدور الذي يحيط بها، وهو أحد عشر، فيكون ثمانية وثلاثين ونصفاً، وهو مساحتها.
إن أحببت، فاضرب القطر، وهو سبعة، في مثله، فيكون تسعة وأربعين، فانقص منها سبعها ونصف سبعها، وهو عشرة ونصف، فيبقى ثمانية وثلاثون ونصف، وهو مساحتها.
فإن قال، عمود مخروط، أسفله أربعة أذرع، في أربعة أذرع، وارتفاعه عشرة أذرع، ورأسه ذراعان في ذراعين.
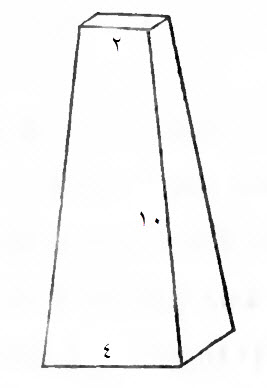
كنا قد بينا، أن كل مخروط محدد الرأس، فإن ثلث مساحة أسفله، مضروباً في عموده، هو تكسيره.
فلما صار هذا غير محدد، أردنا أن نعلم كم يرتفع حتى يفنى رأسه، فيكون لا رأس له.
علمنا، أن هذه العشرة من الطول كله، كقدر الاثنين من الأربعة، فالاثنان نصف الأربعة، فإذا كان ذلك كذلك، فالعشرة نصف الطول، والطول كله عشرون ذراعاً.
لما عرفنا الطول، أخذنا ثلث مساحة الأسفل، وهو خمسة وثلث، فضربناه في الطول، وهو عشرون ذراعاً، فبلغ ذلك مائة وستة أذرع وثلثي ذراع.
نلقى منه، ما زدنا عليه، حتى انخرط.
هو واحد وثلث، الذي هو ثلث مساحة اثنين في اثنين في عشرة، وهو ثلاثة عشر وثلث، وذلك مساحة ما زدنا عليه حتى انخرط.
إذا رفعنا ذلك من مائة وستة أذرع وثلثي ذراع، بقي، ثلاثة وتسعون ذراعاً وثلث، وذلك مساحة العمود المخروط.
وإن كان المخروط مدورا، فالق من ضرب قطره في نفسه، سبعه ونصف سبعه، فما بقي فهو مساحته.
فإن قيل، أرض مثلثة، من جانبيها، عشرة أذرع عشرة أذرع، والقاعدة اثنا عشر ذراعاً.
في جوفها، أرض مربعة. كم كل جانب من المربعة؟
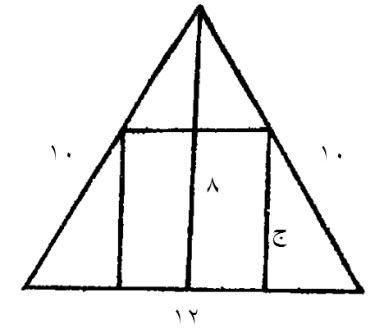
قياس ذلك:
تعرف عمود المثلثة، وهو أن تضرب نصف القاعدة، وهو ستة، في مثله، فيكون ستة وثلاثين، فأنقصها من أحد الجانبين الأقصرين مضروباً في مثله، وهو مائة، يبقى، أربعة وستون، فخذ جذرها ثمانية وهو العمود.
مساحتها، ثمانية وأربعون ذراعاً، وهو، ضربك العمود، في نصف القاعدة وهو ستة.
جعلنا أحد جوانب المربعة شيئاً، فضربناه في مثله، فصار مالاً، فحفظناه.
علمنا، أنه قد بقي لنا مثلثتان، عن جنبتي المربعة، ومثلثة فوقها.
فأمّا المثلثتان، اللتان على جنبتي المربعة، فهما متساويتان، وعموداهما واحد، وهما على زاوية قائمة.
فمساحتها، أن تضرب شيئاً، في ستة إلا نصف شيء، فيكون، ستة أشياء إلا نصف مال، وهو مساحة المثلثتين جميعاً، اللتين هما على جنبتي المربعة.
أمّا تكسير المثلثة العليا، فهو أن تضرب ثمانية غير شيء، وهو العمود، في نصف شيء، فيكون أربعة أشياء إلا نصف مال.
فهذا هو، تكسير المربعة، وتكسير الثلاث مثلثات، وهو، عشرة أشياء، تعدل، ثمانية وأربعين، هو مساحة المثلثة العظمى.
الشيء الواحد من ذلك، أربعة أذرع وأربعة أخماس ذراع، وهو كل جانب من المربعة.