Posted :
The floating point types in C++ are :
float double long double
They are fundamental types , as such they have a mapping to the hardware of a computing machine , so they are as fast , as the machine is capable of performing the computation .
The
floating point types in C++ , are
used to represent numbers
which can
possibly have a fractional part . For example
1 or 1.2 .
The C++ standard , does not specify , the floating point algorithm to be used , this is left to the implementation , but what is typically used , by all implementations , is the IEEE floating point format .

Precision ,
is defined ,
as how many leading 0s
exists in the result of the subtraction ,
of a number desired to be represented , from
the number being actually represented .
Range , is defined , as the possible values , of the available actual numbers , which can be used to represent , a desired number .
Rounding is defined , as the calculated difference , between the desired number , and the actual number .
For example
, if the number to be represented is
3.723 , but the range consist only
of one number , which is 3.73 ,
then the precision is 3.723 - 3.73 = -0.007 ,
which amounts to a precision of three digits , and
the rounding is equal to -0.007 .
This being said , if adding only to the precision digits , assuming that the number which is added has no rounding , rounding is unaffected , as such precision is unaffected . To give an example :
number to be represented : 3.723 actual number represented : 3.73 rounding :-0.007 precision digits : 3 # add a number only to precision digits # so the rounding is not affected 3.723 + 0.09 3.813 3.73 + 0.09 3.82 3.813 - 3.82 -0.007
Subtracting using only the precision digits , assuming that the number being subtracted , has no rounding , does not affect rounding , as such does not affect precision . For example :
number to be represented : 3.723 actual number represented : 3.73 rounding :-0.007 precision digits : 3 # subtract a number which is not # rounded , only from precision # digits so rounding is not affected 3.723 - 0.09 3.633 3.73 - 0.09 3.64 3.633 - 3.64 -0.007
Multiplication , and division , will affect rounding anyhow , and hence precision .
number to be represented : 3.723 actual number represented : 3.73 rounding :-0.007 precision digits : 3 # multiplication by a number beside 0 or 1 3.723 * 2 7.446 3.73 * 2 7.46 7.446 - 7.46 -0.014 # The precision is now of 2 digits , # and the rounding is of 0.014
The
C++ standard , does not define the precision
and range , that floating point types must have .
This is left for the implementation to decide .
What it does define , in order to be compliant with
the C standard , is
some minimal values , such as epsilon ,
which is the difference between 1 , and
the smallest floating point number larger than 1 ,
and which must be for example , for the float
type , FLT_EPSILON , which is equal to 1E-5 .
The
standard also states , that a float
must have a range and a precision less
or equal to
double ,
which itself must have a range and a precision , less or equal
to long double .
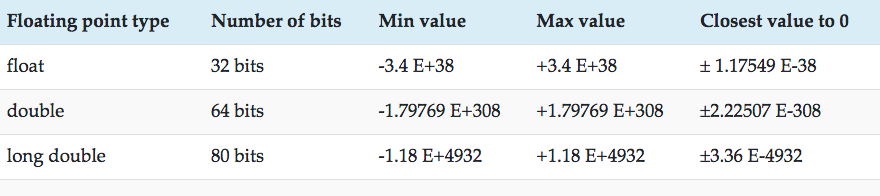
Most implementations , use the IEEE 754 standard , for floating point definition , as such the range and precision of values , is as follows .
An
IEEE
binary floating point number
, has the following
representation : S * M * 2^E .
S represents , the sign .
The sign is represented
in IEEE by using a single bit , which can be
either 0, which represents the +
sign , or 1 , which represents the -
sign .
So in decimal
S can be thought of , as being
-1^S , which is either (-1)^0
which is equal to 1 , or (-1)^1 ,
which is equal to -1.
Mis called the
mantissa , or the significant
, and it has a varying number of bits ,
depending if the IEEE floating point number ,
is what is called a single precision floating point number ,
or a double precision floating point number , or a quadruple
precision floating point number .
For single precision
floating point numbers , which maps
to the C++ float type , the
standard , allocates 23 binary significant bits .
For double precision
floating point numbers , which maps
to the C++ double type , the
numbers of binary mantissa bits allocated
by the standard , are
52 bits .
For quadruple precision
floating point numbers , which
maps to the C++ long double , the number of
binary significant bits allocated
by the standard , are
112 . In practice
long double
is actually implemented , by using
the IEEE extended precision format ,
which states that the significant , must
have at least 63 bits . Intel uses
64 bits .
A floating point number , can be written in one of two forms : Normalized or denormalized . Denormalized is also known as subnormal .
In
normalized ,
it is assumed , that there is an additional
leading
binary digit , which is always set to 1 .
To
illustrate this matter
, float ,
the single precision floating point number
, can be taken as an example .
When in normalized form , instead of
only having 23 significant
digits , with the assumed leading 1
bit , a single precision floating point
number actually has 24 bits .
When
all these
bits are set to 1 , the max
value that can be stored is :
1 + 2^-1 + 1 * 2^-2 + ... + 1 * 2^-23 .
which is equal to
1 + 1/2 + 1/4 + 1/8 + ... + 1/8'388'608 ,
which is equal to
1 + 2^22 / 2^23 + 2^21 / 2^23 + 2^20 / 2^23 ... + 2^0 /2^23
which is equal to
1 + 8'388'607 / 8'388'608
which is equal to 16'777'215 / 8'388'608 .
The
other available range values , are
as such : 1 + setting bits of the significant
to 1 . For example 1 + 2^-1 , yield
the number 1.5 , 1 + 2^-2
yield the number 1.25 ...
Taking
into consideration the leading sign bit ,
the maximum and minimum range values are :
- 16'777'215 / 8'388'608 and
16'777'215 / 8'388'608 .
Other range values are : -1.25 ,
1.5 , and 1.75 ...
Range
values have full precision , meaning , if a desired
number is to be represented using a value in the range ,
then the rounding is of 0 .
Concerning
E , or the
exponent , it has a variable
number of bits , depending on the IEEE
floating point format , being used .
For
what is called single precision floating point format ,
there are
8 bits reserved
for the
exponent .
For
what is called , double precision format , there are
11 bits reserved for the exponent .
For
what is called , quadruple precision format , there
are
15bits reserved
for the exponent . The extended format , specifies , that
at least 15 bits must be reserved for the exponent .
If
float , is to be
taken as an example
, the max value
of the exponent is as such 2^8 - 1 . Hence
2 can only be raised to exponents between
0 and 255, which
means if exponent is used as is , then it is
only possible
to use positive values , of the exponent .
But ,
what is actually wanted
, is to have negative values
of the exponent , and values to be used for
special purposes , such as : denormalized
form , or other cases .
As such the IEEE standard ,
reserved the two special case of having all bits of exponents
set to 0 , or to 1 , for the
special purposes .
To have negative values of the exponent , in normalized form , the standard introduced the concept of bias.
Bias
is simply the
max value of the exponent , divided
by 2 , and only the integer part is kept .
Hence for 8 bits , the max value of the
exponent is 255 , and the
bias is the integer division of 255 by 2 ,
which is equal to 127 .
Having
bias in hands , and
to get negative values
for the
exponent , the only
road of action , is to subtract the possible values of the
exponent , which are between 1 and 254 ,
since all 0 , and all1 are reserved
for special purposes , from the bias .
This leads to having an exponent , which
can have values between
-126 , and 127 ,
for single precision floating point numbers ,
in normalized form .
This
being said , the min exponent value in normalized form ,
is as such -126 , and the max exponent value
in normalized form is 127 .
So when raising 2 to the power of these exponents ,
it can have values of :
... 2^-3 2^-2 2^-1 2^0 2^1 2^2 2^3 ... ,
which is equal to ...1/8 1/4 1/2 1 2 4 8 ... .
Hence the
smallest power of two , that can be gotten in normalized
form is 2^-126 , which is equal to
1/85070591730234615865843651857942052864 ,
and the largest power of two , that can be gotten
in normalized form , is 2^127 , which is
equal to 170141183460469231731687303715884105728 .
This
being said ,
range has just got
broader .
The max range value that can be gotten in normalized form ,
is as such :
16777215/8388608 * 170141183460469231731687303715884105728 ,
which is equal to :
340282346638528859811704183484516925440 , which is :
3.4028235 E+38 ,
and the closest value to 0
is as such : 1 * 1/85070591730234615865843651857942052864 ,
which is equal to :
1.1754944E-38 .
When
exponent bits are all set to 1 , and the
significant bits are all zero , then , by the standard ,
this
represents an infinite
value , which can be , negative infinity ,
if the sign bit is 1 , or positive infinity , if the
sign bit is 0 .
When
exponent bits are all set to 1 , and any significant
bit is not set to 0 , by the standard , this represents
a not a number value , like for example ,
adding positive and negative
infinity , yields a not a number .
When
exponent bits are all set to 0 , then
the significant bits are in a denormalized form ,
so there is no leading assumed binary 1 bit ,
and the number of significant digits ,
are precisely the number specified by the standard .
The
exponent being all set to 0 , this means
that it must
have a fixed value
, which is equal to
1 - bias , where bias as stated earlier ,
is the max value of the exponent bits ,
divided by 2 , and the fractional part
discarded .
Taking
float as an
example ,
in denormalized form , the exponent has a fixed value of
1 - ( 255 / 2 ) = 1 - 127 = -126 .
This means that for a float , when in a denormalized form ,
the closest value to 0 is 2^-23 * 2^-126
which is equal to 2^-149 which is equal to
1/713623846352979940529142984724747568191373312 .
The
question ,
why the range does not contain this
denormalized value , as being the closest one to
zero , is answered by , because usually
a denormalized form has a performance cost ,
and processors are set to truncate , a
subnormal form to 0 .
Just a quick note , for Intel microprocessors , when the floating point format is the extended one , the leading bit is not assumed , but all what was talked about in this section , remains the same . So the principle for IEEE floating point format , is the same .
Floating point literals can be written either in decimal , or in hexadecimal notation .
When written in decimal notation , they can be written either in scientific or regular decimal notation .
Scientific notation can be more compact to use ,
in certain circumstances , for example 1E12 ,
is clearer , and more compact , than 1000000000000.0 .
If , it is still preferred not to use the scientific format ,
and
to make things clearer ,
a single quote ' , can be used to separate
any kind of numbers in C++ , hence the earlier
example , can be rewritten as 1'000'000'000'000.0 or
as 1'0000'0000'0000.0 .
By
default a floating point number literal ,
is of type
double ,
if suffixed with an f , case
insensitive , it is of type float ,
and if suffixed by an l , case
insensitive , it is of type long double .
It is not necessary for a floating point literal ,
to be stored exactly as written .
The syntax for writing decimal floating point is :
d+.d* d*.d+ d+[.]ed+
Where d is any digit between 0-9 ,
+ means one or more , *
means zero or more , what is between []
is optional , and e is case insensitive ,
and means
an exponent of the number 10 . For
example :
double var_d; var_d = 1. ; var_d = .1 ; var_d = 1.0 ; var_d = 1e1 ; var_d = 1.e1 ; var_d = 1.1e1 ; var_d = .1e1 ;
A floating point literal , can also be written in hexadecimal , using the following notation :
0xh+[.]h*Pd+ 0xh*.h+Pd+
Where 0xis case insensitive ,
and stands for hexadecimal , his an hexadecimal
digit between 0-F , +
means one or more , what is
between [] is optional ,
* means zero or more ,
and P is case insensitive ,
and means 2 to the power p ,
and d is one or more digits between 0-9 .
As an example :
double var_d ; var_d = 0xfP0; // 15.0 var_d = 0Xf.P0; // 15.0 var_d = 0xf.0P0; // 15.0 var_d = 0X.1P0; // 1/16 = 0.062500 var_d = 0x.1p1; // (1/16) * 2 = 0.125000
To
print floating point literals , printf from
C , or cout from C++
can be used .
When using printf
, a format specifier
must be provided
,
and a length modifier can optionally be prepended ,
to the format specifier .
As
such to
convert a float
or a double
number , to a character string in decimal notation ,
%f must be used .
As for long double ,%Lf
must be used , where L
must be capital . L is called the
length modifier , and f is called
the format specifier .
If
it is desirable to convert a float or
a double , to a
character string in
scientific notation , then %e can be used for
float , and double , as for
long double %Le must be used , where
L is capital .
If
it is desirable , to
let printf decides
if the f , or e format
specifiers are to be used , then %g can be used .
%g does not output a trailing decimal point ,
or trailing zeroes .
If
it is desirable , to print the exponent
in capital letter , then
capital E , or
capital G , are to be used .
When
printing a floating point number using printf ,
the default number of digits shown
is 6 . For %f or %e ,
the count starts after the decimal point .
For
%g , there is an
algorithm to decide
the number of digits to be shown after the decimal point ,
and if %f or %e should be used .
The algorithm is as follows . The number
is first written
in scientific form . For example
1'43'21'2 is written as 1.43212 * 10^5 .
Given the set number of digits to be shown , the default
being 6 , and if set to 0 , then
it is assumed to be 1 , the number of digits to be shown
is compared with the resultant power
of writing the number in scientific form .
If it is larger than the gotten power ,
and the gotten power is larger or equal to -4 , then
the number is written using %f , and the number of
digits to be shown after the decimal point , is the set
number of digits to be shown minus one , minus the gotten power .
So for 1'43'21'2 , assuming the default
number of digits to be shown is 6 ,
6 is larger than 5 , which
is the power gotten for writing this number in
scientific form , 5 is larger than
-4 , hence the number is displayed using %f ,
and the number of digits after the decimal point to be shown is
6 - 1 - 5 = 0 , so 1'43'21'2
is displayed as
143212 .
Otherwise , the number is
displayed using
%e , and the number of digits to
be shown after the decimal point , is the set
number of digits , minus one .
To specify the number of digits ,
the length modifier can be preceded by
.n ,
where n is to be replaced by the desired number
of digits to be shown .
#include <stdio.h>
int main (void ){
printf ("%f\n" , 123'456'789'123'456'789.0 );
/* %f is used , the number of digits
to be shown is not set , hence the
default number of digits to be shown
after the decimal point is 6 .
Output :
123456789123456784.000000 */
printf ("%e\n" , 123'456'789'123'456'789.0 );
/* %e is used , the number is to
be written in scientific form ,
and only six decimal digits
are to be shown after the decimal
point . Hence
the output is :
1.234568e+17 */
printf ("%.8E\n" , 123'456'789'123'456'789.0 );
/* %E is used , hence the number is
to be displayed in scientific
format , and exponent is to be
capitalized .
The number of digits to
be shown after the decimal point
is set to 8 , hence what is
displayed :
1.23456789E+17 */
printf ("%G\n" , 123.23467 );
/* %G is used , the default number
of digits to be shown is 6 .
First 123.23467 , is written in
scientific format as
1.2323467 * 10^2 , so the power is
2 .
6 > 2 > -4 , hence %F is to be
used , and the number of digits
to be shown after the decimal
point are 6 - 1 - 2 = 3
As such the result is :
123.235 */
printf ("%g\n" , 1'232'346.7 );
/* %g is used . Hence first the
number is written in
scientific notation as
1.2323467 * 10^6 .
6 = 6 > -4 , so what must be
used is %e , and the number
of digits to be shown
after the decimal point are
6 - 1 = 5 , hence the output
is :
1.23235e+06 */
printf ("%f\n" , 1'234'56.0 );
//123456.000000
printf ("%g\n" , 1'234'56.0 );
/* %g , or %G , do not output
trailing decimal point or 0's
123456 */ }
To
convert floating point numbers ,
to a string of hexadecimal
characters , the format specifiers a ,
or A ,
can be used , where A will output capital case characters ,
and a will output lowercase characters .
#include <stdio.h>
int main (void ){
printf ("%a\n" , 1'123.0 );
// 0x1.18cp+10
printf ("%A\n" , 1'123.0 );
/* 0X1.18CP+10 */ }
In
addition to printf which prints the
formatted characters to standard output ,
fprintf can be used to print the
formatted characters to a file ,
and sprintf can be used to
store the formatted characters into a
buffer , which is
just a memory area of typechar .
snprintf can be used for preventing
buffer overflow , by
limiting the number of
characters to be stored in the buffer .
printf_s , fprintf_s
, sprintf_s ,
snprintf_s
are just the same functions , but with just some
additional error handling
.
When using cout ,
to convert floating point numbers to characters ,
the default number of output digits , is 6 .
and the output default format is defaultfloat .
Basically defaultfloat , counts both the
digits before , and
after the decimal point , as being part of the number of digits
displayed . When the number of digits is larger than the one
set , rounding and exponential notation might occur .
Using
scientific
, scientific output format
can be set , in scientific format ,
only the digits after the decimal points
are counted , the exponential notation is always
used , and rounding might occur .
Using
fixed ,
fixed output format could be set .
In fixed format , only digits are used for
output , and only the digits after the decimal point are counted .
When the number to be displayed , has a larger number of
digits , then the set one , rounding occurs .
Using
hexfloat , the floating
point number is converted
to its hexadecimal floating point
number format ,
the one described earlier in floating
point literals .
#include <iostream>
#include <iomanip>
int main (void ){
std ::cout << std ::cout .precision ( ) << std ::endl ;
/* Get the set number of digits for output
Output :
6 .*/
std ::cout << 1'234'567.0 << std ::endl;
/* By default std ::defaultfloat is
set , hence the output format
counts the digits before , and after
the decimal point . The number
of digits to output is 6 ,
hence rounding occurs based
on the seventh digit , and exponential
notation is used .
Output :
1.23457e+06 */
std ::cout << 1.0 << std ::endl;
/* 1 */
std ::cout << std ::scientific;
/* Set the output format to scientific .*/
std ::cout << 1'234'567.0 << std ::endl;
/* When output format is set to scientific ,
only the digits after the decimal points
are counted , hence six decimal digits
after the decimal point are represented ,
no rounding occurs , as in the
defaultfloat case .
Output :
1.234567e+06 */
std ::cout << 1.0 << std ::endl;
/* Output :
1.000000e+00 */
std ::cout << std ::fixed;
/* Set the output format to fixed */
std ::cout << 1'234'567.0 << std ::endl;
/* Output format being fixed , only digits are
used for the output , the number of digits
is counted starting after the decimal point .
Output :
1234567.000000 */
std ::cout << 1.0 << std ::endl;
/* Output :
1.000000 */
std ::cout << std ::hexfloat;
/* Set output format to hexadecimal float .*/
std ::cout << 1'234'567.0 << std ::endl;
/* Output :
0x1.2d687p+20 */
std ::cout << 1.0 << std ::endl;
/* Output
0x1p+0 */}
The
default number of digits to be printed , can be
set and gotten ,
using precision .
#include <iostream>
int main (void ){
std ::cout << std ::cout .precision ( ) << std ::endl;
/* Get the number of digits to display .
Output :
6 */
std ::cout << 123456.0 << std ::endl;
/* Number of digits to display is 6 ,
std ::defaultfloat is used by
default , hence numbers before , and
after the decimal point are counted .
Output :
123456 */
std ::cout .precision (3 );
/* Set the number of digits to display to 3 */
std ::cout << 123456.0 << std ::endl;
/* The number of digits to display is
set to 3 . defaultfloat is being
used , hence digits before and after
the decimal point , are counted
Output :
1.23e+05 */ }
The
advantages of
cout
over the printf family
is that cout is type aware ,
so there is no need to specify any type .
The
problem with cout ,
is that it is not really nice to use ,
when formatting strings , like printf
is .
To remedy this problem ,
the C++ 20 standard ,
introduced the header
format ,
which defines text formatting functions
and classes .
The
format function , which is
part
of the C++ 20 format header ,
can be used as sprintf ,
to get formatted strings .
As of
march 2021 , this header is not yet
implemented by any compiler .
#include <format>
#include <iostream>
int main ( ){
double var_d = 1234567.0;
std ::cout << std ::format ("{0 } , {0:f } {0:e } {0:g }" , var_d );
/* 0 is the index of the argument , in this case , there is only
1 , which is var_d .
f , is the fixed format talked about earlier .
e , is the exponential format , talked about earlier .
g , is the general format , which is the defaultfloat , talked about earlier */ }
Meta information
about numbers , can be gotten using
the headers : climits , cfloat
and limits .
The
climits and the cfloat
headers
originate in the C standard , where
they are named :
limits
, and float
.
The
climits header
can be used to get meta information about
integer types .
For example , for a given machine , what are the min
and max values of an int , or
of an unsigned long , or what is the
number of bits in a char .
#include <iostream>
#include <cstdio>
#include <climits>
int main (void ){
std:: cout << INT_MIN << std:: endl;
// -2147483648
std:: cout << INT_MAX << std:: endl;
// 2147483647
printf ("%d\n" , CHAR_BIT );
/* 8 */ }
The
cfloat header contains
meta information , related to floating point
implementation , such as the min or max value , of
float , or of double ..
#include <iostream>
#include <cfloat>
int main (void ){
std ::cout <<FLT_MAX <<" : float range , absolute value \n";
/* For double DBL_MAX can be used , and for long double ,
LDB_MAX can be used .
Output :
3.40282e+38 : float range , absolute value */
std ::cout <<FLT_MIN <<" : float closest value to 0 normalized \n";
/* For double and long double , DBL_MIN ,
and LDBL_MIN can be used .
Output :
1.175494e-38 : float closest value to 0 normalized */
std ::cout <<FLT_TRUE_MIN <<" : float closest value to 0 denormalized \n";
/* For double , and long double ,
DBL_TRUE_MIN , and LDBL_TRUE_MIN
can be used .
This macro does not seem to be supported
on some compilers .
Output :
1.4013e-45: float closest value to 0 denormalized .*/
std ::cout <<FLT_MANT_DIG <<" . float number mantissa digits \n";
/* Display the number of binary digits of the mantissa in
normalized form .
For double , and long double , DBL_MANT_DIG ,
and LDBL_MANT_DIG can be used .
Output :
24 : float number mantissa digits : */
std ::cout <<FLT_DIG
<<" : float mantissa digits , map to : "
<<" FLT_DIG decimal digits"
<<std ::endl;
/* This is just , how mantissa digits in
denormalized form , so without assuming
an implicit one , map to decimal digits .
For example , float has 23 mantissa digits ,
in denormalized form , this maps to 23 multiplied
by log of 2 to the 10th base , which is
equal to ~ 6 .
How come this formula ? Simply put , since
what is needed , is the corresponding number of
digits , when passing from base 2 to base 10 ,
the question to ask is , how many each digit
of base 2 , maps to digits in base 10 .
The answer is logarithm in base 10 of 2 , which
is how many digits 2 , yield in base 10 .
Logarithm of 2 , to the base 10 , is around
0.30101299 , which means that 10 raised to
this power yield 1.999921687556491 .
Having how each digit in base 2 , maps to a digit
in base 10 , multiplying this by
the number of digits in base 2 ,
yields the number of
digits in base 10 , which is
23 multiplied by ~ 0.3010299 , which is
equal to about 6.923689900271567 ,
which is about 6 digits , or 10
to the power 6 .
For double , and long double , DBL_DIG ,
and LDBL_DIG can be used .
Output :
6 . float mantissa digits , map to : FLT_DIG decimal digits */
std ::cout <<FLT_MAX_EXP
<<" : float largest positive power of 2 plus one \n";
/* Outputs the value of the floating point
number , max positive power of 2 , plus one .
For double , and long double ,
DBL_MAX_EXP , and LDBL_MAX_EXP
can be used .
Output :
128 : float largest positive power of 2 plus one */
std ::cout <<FLT_MAX_10_EXP
<<" : float largest positive power of 10 \n";
/* Having from earlier , the largest positive
power plus one , of 2 , for a floating point
number , FLT_MAX_10_EXP provides the max
power of 10 .
DBL_MAX_10_EXP , and LDBL_MAX_10_EXP ,
can be used to get the values
for double , and long double .
Output :
38 : float largest positive power of 10 */
std ::cout <<FLT_MIN_EXP
<<" : float , smallest negative power of two plus one \n";
/* Output the value of the floating point
number , least negative power of two ,
plus one .
For double , and long double , DBL_MIN_EXP ,
and LDBL_MIN_EXP can be used .
Output ;
-125 : float , smallest negative power of two plus one */
std ::cout <<FLT_MIN_10_EXP
<<" : float , smallest negative power of 10 \n";
/* Having the least negative power of
two for a floating point number ,
FLT_MIN_10_EXP ,provides the
least negative power of 10 .
DBL_MIN_10_EXP and LDBL_MIN_10_EXP
can be used to get the values
for double , and long double .
Output :
-37 : float , smallest negative power of 10 */
std ::cout <<FLT_RADIX
<<" : float base is \n";
/* The base of the floating point type .
For double , and long double ,
DBL_RADIX , and LDBL_RADIX can be
used .
Output :
2 : float base is */
std ::cout <<FLT_EPSILON
<<" : float FLT_EPSILON value is \n";
/* Returns the difference between one
, and the smallest floating point
number , larger than one .
Output :
1.19209e-07 : float FLT_EPSILON value is */
std ::cout <<FLT_HAS_SUBNORM
<<" : float FLT_HAS_SUBNORM supports denormalized values \n";
/* FLT_HAS_SUBNORM , will return 1 , if
float supports denormalized values ,
0 if float does not support denormalized
values , and -1 , if this cannot be
determined .
DBL_HAS_SUBNORM and LDBL_HAS_SUBNORM
can be used for double , and long double
types .
This macro does not seem to be supported
by compilers .
Should output :
1 : float FLT_HAS_SUBNORM supports denormalized values */
std ::cout <<FLT_EVAL_METHOD
<<" : floating point types eval method is FLT_EVAL_METHOD\n";
/* Returns the floating point types eval method .
2
means arithmetic operations are performed by promoting
the operands to the long double type .
1
means arithmetic operations are performed by promoting
the operands to long double , if any operand is of the
long double type ,
otherwise operands are promoted to the double type ,
even if both operands are of the float type .
0
means arithmetic operations are done in the
type of the widest operand .
-1
means it is indeterminable
Output :
0 : floating point types eval method is FLT_EVAL_METHOD */
std ::cout <<FLT_ROUNDS
<<" : floating point types round mode is FLT_ROUNDS\n";
/* returning the floating point types rounding mode ,
rounding is done in binary .
-1
means it cannot be determined .
0
means rounding is performed towards
0 . For example -1.2 will be rounded
to -1 , and 1.2 to 1 .
1
means rounding is performed to the nearest
value , when in between , rounding is done
towards even . For example -1.2 , is rounded
to -1 , -1.8 to -2 , and -1.5 to -2 .
2
means round towards positive infinity .
For example -1.2 rounds towards -1 ,
and 1.2 to 2 .
3
means round towards negative infinity .
For example , -1.2 rounds to -2 , and
1.2 to 1 .
Output :
1 : floating point types round mode is FLT_ROUNDS */ }
The limits header
defined by the C++ standard , contains
the numeric_limits class .
The numeric_limits class can be
used to get meta information , related to
both the integral , and floating point types .
All the information in both climits , and
cfloat , can be gotten
using numeric_limits , plus additional information .
#include <limits>
#include <iostream>
int main (void ){
std ::cout <<std ::numeric_limits <float > ::min ( ) <<std ::endl;
/* For floating point types , min is the closest value
to 0 , this corresponds to FLT_MIN in the cfloat
header .
Output :
1.17549e-38 */
std ::cout <<std ::numeric_limits <int > ::min ( ) <<std ::endl;
/* For integer types , this is the smallest negative value .
Output :
-2147483648 */
std ::cout <<std ::numeric_limits <float > ::lowest ( )
<<" : "
<<std ::numeric_limits <float > ::max ( )
<<std ::endl;
/* For floating point type , max provides
the same result as FLT_MAX , lowest is just
max multiplied by -1 .
Output
-3.40282e+38 : 3.40282e+38.*/
std ::cout <<std ::numeric_limits <int > ::lowest ( )
<<" : "
<<std ::numeric_limits <int > ::max ( )
<<std ::endl;
/* For integer types , lowest , and min are the same ,
which is , the smallest negative value , max is the
largest positive value representable in this
integer type .
-2147483648 : 2147483647 */
std ::cout <<std ::numeric_limits <float > ::digits
<<" : "
<<std ::numeric_limits <float > ::digits10
<<std ::endl;
/* digits is the same as FLT_MANT_DIG , whereas
digits10 is the same as FLT_DIG .
Output :
24 : 6 */
std ::cout <<std ::numeric_limits <int > ::digits
<<" : "
<<std ::numeric_limits <int > ::digits10
<<std ::endl;
/* For integer types digits output , the number
of bits allocated , minus the number of sign
bits or padding bits , and
digits10 , how digits map
to decimal digits .
Output :
31 : 9 */
std ::cout <<std ::numeric_limits <float > ::min_exponent
<<" : "
<<std ::numeric_limits <float > ::min_exponent10
<<std ::endl;
/* For floating point types , min_exponent is
the same as FLT_MIN_EXP , and
min_exponent10 is the same as FLT_MIN_10_EXP .
Output :
-125 : -37 */
std ::cout <<std ::numeric_limits <int > ::min_exponent
<<" : "
<<std ::numeric_limits <int > ::min_exponent10
<<std ::endl;
/* For integer types , min_exponent
and min_exponent10 return 0 .
Output :
0 : 0 */
std ::cout <<std ::numeric_limits <float > ::max_exponent
<<" : "
<<std ::numeric_limits <float > ::max_exponent10
<<std ::endl;
/* For floating point types , max_exponent is
the same as FLT_MAX_EXP , and
max_exponent10 is the same as FLT_MAX10_EXP .
Output :
128 : 38 */
std ::cout <<std ::numeric_limits <int > ::max_exponent
<<" : "
<<std ::numeric_limits <int > ::max_exponent10
<<std ::endl;
/* For integer types , max_exponent ,
and max_exponent10 return 0 .
Output
0 : 0 */
std ::cout <<std ::numeric_limits <float > ::radix <<std ::endl;
/* For floating point types , radix is the
same as FLT_RADIX , which is the floating
point type , digits , base .
Output :
2 .*/
std ::cout <<std ::numeric_limits <int > ::radix <<std ::endl;
/* For integer types , this is the base for the
digits .
Output :
2 .*/
std ::cout <<std ::numeric_limits <float > ::epsilon ( ) <<std ::endl;
/* For floating point numbers , this is
the same as FLT_EPSILON or DBL_EPSILON
or LDBL_EPSILON , depending on if
std ::numeric_limits <float > ::epsilon ( ) , or
std ::numeric_limits <double > ::epsilon ( ) , or
std ::numeric_limits <long double > ::epsilon ( )
are used .
Output :
1.19209e-07 */
std ::cout <<std ::numeric_limits <int > ::epsilon ( ) <<std ::endl;
/* For integer types , this results in 0
Output :
0 */
std ::cout <<std ::numeric_limits <float > ::round_style <<std ::endl;
/* round_style returns the rounding style , used
by this numeric type . rounding is done in
binary .
The rounding style can be one of the values ,
defined in the enum float_round_style , which
is part of the limits header .
round_indeterminate , which has a value of
-1 , means that the rounding style cannot be
determined .
round_toward_zero , which has a value of 0 :
for example -1.2 is rounded towards -1 ,
and 1.2 is rounded towards 1 .
integral types usually have this mode .
round_to_nearest , which has a value of 1 :
for example -1.2 is rounded towards -1 ,
and -1.7 is rounded towards -2 whereas
half way cases are rounded towards even ,
so -1.5 is rounded to -2 , and 1.5 is
rounded to 2 .
Floating point types , usually have
this rounding mode .
round_toward_infinity , which has a value of
2 :
for example -1.2 is rounded to -1 ,
and 1.2 is rounded towards 2 .
round_toward_neg_infinity , which has a value
of 3 .
for example -1.2 is rounded to -2 ,
and 1.2 is rounded to 1 .
Output :
1 .
Hence the rounding style for float is
round to the nearest on this machine .*/
std ::cout <<std ::numeric_limits <int > ::round_style <<std ::endl;
/* Print the rounding mode for int ,
integral types usually round toward
0 , which is the round_toward_zero
mode , which has a value of 0 .
Output :
0 */
std ::cout <<std ::numeric_limits <float > ::round_error ( ) <<std ::endl;
/* Returns the largest possible rounding error
which depending on the rounding mode , can be
for example 0.5 when rounding to the nearest ,
or 1 when rounding towards 0 .
Output :
0.5 */
std ::cout <<std ::numeric_limits <int > ::round_error ( ) <<std ::endl;
/* For integral types , round_error returns 0
Output :
0 */
std ::cout <<std ::numeric_limits <float > ::has_denorm <<std ::endl;
/* has_denorm , returns an enum value , of type
float_denorm_style , which indicates ,
if the type supports , denormalized
form .
denorm_indeterminate has a value of - 1 ,
this indicates that it cannot be determined
whether or not the type supports
denormalized form .
denorm_absent which has a value of 0 ,
indicates , that the type does not support
denormalized form . integral types
usually do not support denormalized
style .
denorm_present which has a value of 1 ,
indicates , that the type support
denormalized form , floating point types
usually support denormalized form .
float_denorm_style is part of the limits
header .
Output :
1 */
std ::cout <<std ::numeric_limits <int > ::has_denorm <<std ::endl;
/* For integral types , has_denorm usually
returns 0 , which is false .
Output :
0 */
std ::cout <<std ::numeric_limits <float > ::denorm_min ( ) <<std ::endl;
/* denorm_min , returns the smallest
possible denormalized value , which is
for float : 2^-149 .
Output
1.4013e-45 */
std ::cout <<std ::numeric_limits <int > ::denorm_min ( ) <<std ::endl;
/* denorm_min , returns 0 for integral
types */
std ::cout <<std ::numeric_limits <float > ::has_infinity <<std ::endl;
/* has_infinity returns true , if a type supports
infinity , this is true for floating point types ,
and false for integral types .
Output :
1 */
std ::cout <<std ::numeric_limits <int > ::has_infinity <<std ::endl;
/* Check if the int type has infinity ,
Output :
0 */
std ::cout <<std ::numeric_limits <float > ::infinity ( ) <<std ::endl;
/* infinity returns for floating point types ,
the value positive infinity , and for
integral types , it returns 0
Output :
inf */
std ::cout <<std ::numeric_limits <int > ::infinity ( ) <<std ::endl;
/* Get the positive infinity value for
the int type ,
Output :
0 */}
The
header cmath ,
originates from the
C
standard , where it is named
math . It contains macros , and
mathematical functions , that
might be useful .
For example , it can be used to
calculate floating point modulo , using
the fmod function . Floating point modulo
is not support by the modulo % operator .
It can also be used to calculate , logarithm , power
, hypotenuse , sin , cos , tang ... or for rounding ,
such as by using ceil , floor ,
or trunc ... or for classifying a floating
point
number , such as , is it infinity , is it not a number ...
or for extracting information
from floating point numbers , such as , its fractional and
non fractional parts ...
It also contains , some specialized mathematical functions, to calculate for example , exponential integral .
#include <iostream>
#include <cmath>
int main (void ){
std ::cout <<std ::fmod (3.1 , 1.1 ) <<std ::endl;
/* fmod provides modulo for floating point types .
fmod is overloaded , for float , double , and long
double .
3.1 is a double literal , hence the double
version is called .
Output :
0.9 */
std ::cout <<std ::log10 (2.0 ) <<std ::endl;
/* Calculate log10 of 2.0 , log10 is overloaded ,
for float , double , and long double arguments .
The double version is called , since 2.0 is
of the double type .
Output :
0.30103 */
std ::cout <<std ::pow (10.0 , std ::log10 (2.0 ) ) <<std ::endl;
/* Calculate 10.0 to the power of 0.30103 ,
which is equal to 2.0 .
The pow function is overloaded to accept
arguments of type float , double , and long
double .
Output :
2 */
std ::cout <<(std ::fpclassify (2.0 ) == FP_NORMAL ? "FP_NORMAL" : "Other" )
<<std ::endl;
/* Classify the floating point type returning an
integer , which can be one of the following :
FP_NORMAL :
indicates , that the floating
point value , is not denormalized or
0 , or infinite , or not a number .
FP_SUBNORMAL :
indicates , that the floating point
value , is denormalized .
FP_ZERO :
indicates , that the floating point
value is 0 .
FP_INFINITE :
indicates , that the floating point
value , is infinite .
FP_NAN
indicates , that the floating point
value , is not a number .
Output :
FP_NORMAL */
double part_fractional { }; /* Initialize the double variable with 0 */
double part_nonFractional { }; /* Initialize the double variable with 0 */
part_fractional = std ::modf (1.31 , &part_nonFractional );
/* Call the modf function , which extracts
the fractional , and non fractional part
of a floating point number .
modf is overloaded , so it can operate ,
on double , and long double arguments .*/
std ::cout <<"1.31 = " <<part_nonFractional <<" + "
<<part_fractional
<<std ::endl;
/* Output :
1.31 = 1 + 0.31 */
std ::cout <<std ::expint (3 ) << std ::endl;
/* exponential integral has the formula of :
integral from minus x to infinity of (1/t )
* e^-t dt
Output :
9.93383 .*/ }
The
cmath header , also
defines some macros . For example , it defines
INFINITY , which
represents positive infinity , and
NAN , which represents not a number .
It
also defines , the macro math_errhandling ,
which can be used to check how floating point
functions , and operators , report errors .
When
math_errhandling has a value
of the macro MATH_ERRNO , which evaluates
to 1, then error reporting is done ,
by setting
a value inside the global variable errno ,
which is part of the cerrno header .
When
math_errhandling has a value
of the macro MATH_ERREXCEPT , which evaluates
to 2 , then error reporting is done , by
checking exceptions using
fetestexcept , which is part
of the cfenv header .
When
math_errhandling has a value
of MATH_ERREXCEPT|MATH_ERRNO , which evaluates
to 3 , then both
methods are
used to report errors
.
Not
all math
library functions , support
both error reporting mechanism .
Some just support setting errno ,
others just support exceptions ,
some do not support any ,
some supports both error reporting mechanism .
When
using the functions defined in the
fenv header , the directive
#pragma STDC FENV_ACCESS ON ,
must be set
, be
it globally or locally .
To
check for errors , and
before performing any
floating point operation
, errno must be set
to 0 , and all floating point exceptions must be
cleared using feclearexcept (FE_ALL_EXCEPT ); .
Once
this is done , and after a floating point
operation has been performed ,
if errno has a non zero
value or if fetestexcept (FE_ALL_EXCEPT ); returns non zero ,
then this
means that an error
has occurred .
If fetestexcept (FE_INVALID ) returns
non zero or if errno == EDOM ,
this means , that a function was provided
an argument , which value is not
acceptable , as in sqrt (-1 ) . This
type of error , is called a domain error.
If
fetestexcept (FE_DIVBYZERO )
returns non zero , or errno == ERANGE ,
then this means that an exact infinite value
was gotten , for example 1 / 0.0 .
In thus case , the function returns HUGE_VAL
, or HUGE_VALF , or HUGE_VALL ,
depending if it should return a double , a float or a
long double . This kind of error is called
a pole error .
If
fetestexcept (FE_OVERFLOW ) returns non zero ,
or if errno == ERANGE
then the result is too large to be stored in
the given floating point type , but is finite ,
for example exp (10000.0f ) .
This type of error is called overflow .
The library function in such case
returns one of HUGE_VAL ,
HUGE_VALF or HUGE_VALL ,
depending
on if its return type is
: double ,
float or long double .
If
fetestexcept (FE_UNDERFLOW ) returns
non zero , or if errno == ERANGE ,
then the result is too small to be stored in the
destination type , even after rounding , where
it becomes 0 or subnormal ,
for example exp (-10000.0f ).
Typically when underflow occurs,
floating point functions returns 0.0 .
If
fetestexcept (FE_INEXACT )
returns non zero , then the
result had to be rounded
to fit in the destination type .
#include <iostream>
#include <cmath>
#include <cfenv>
#pragma STDC FENV_ACCESS ON;
/* Inform the compiler that
functions in the fenv header
will be used .*/
int main (void ){
double var_d { };
std ::cout <<math_errhandling
<<" . Error report mechanism is : math_errhandling \n";
/* Check which error reporting mechanism is set
for cmath library functions .
1
means errors are reported using the global
variable errno .
2
means errors are reported by checking for
exceptions
3
means both methods can be used .
Output :
3 . Error report mechanism is : math_errhandling */
/* Clear errors before performing an operation */
feclearexcept (FE_ALL_EXCEPT );
errno = 0 ;
std ::cout << std ::boolalpha ;
/* Set cout to display boolean values
using true or false */
sqrt (- 1 );
/* Calculate the square root of -1 */
std ::cout <<(errno == EDOM ) << " | "
<<(fetestexcept (FE_INVALID ) != 0 )
<<std ::endl;
/* Check if EDOM or if FE_INVALID are set
Output
true | true */
/* Clear errors before performing an operation */
feclearexcept (FE_ALL_EXCEPT );
errno = 0 ;
var_d = 1 / 0.0 ;
std ::cout <<(errno == ERANGE ) << " | "
<<(fetestexcept (FE_DIVBYZERO ) != 0 )
<<std ::endl;
/* Check if ERANGE or if FE_DIVBYZERO
are set
Output :
false | true */
/* Clear errors before performing an operation */
feclearexcept (FE_ALL_EXCEPT );
errno = 0 ;
exp (10000.0f );
std ::cout <<(errno == ERANGE ) << " | "
<<(fetestexcept (FE_OVERFLOW ) != 0 )
<< std ::endl;
/* Check if ERANGE or FE_OVERFLOW errors .
Output :
true | true */
/* Clear errors before performing an operation */
feclearexcept (FE_ALL_EXCEPT );
errno = 0 ;
exp (-10000.0f );
std ::cout <<(errno == ERANGE ) << " | "
<<(fetestexcept (FE_UNDERFLOW ) != 0 )
<< std ::endl;
/* Check for ERANGE and FE_UNDERFLOW errors .
Output :
true | true */}
In
addition to using
FLT_ROUNDS
from the
cfloat header
, and
round_style
from numeric_limits ,
in the limits
header
,
to get the rounding mode
, the header cfenv ,
provides the fegetround
method , to query for the rounding mode ,
and the function fesetround ,
to set the rounding mode .
fegetround
returns an integer
value , which map to one of the
macros
FE_DOWNWARD ,
which means round
towards negatives infinity ,
FE_UPWARD , which means
round towards positive infinity ,
FE_TONEAREST , which means
round towards the nearest value
and on tie round towards the even
value ,
FE_TOWARDZERO ,
which means round toward 0 .
fesetround can
set the rounding mode
using one of
FE_DOWNWARD ,
FE_UPWARD ,
FE_TONEAREST ,
FE_TOWARDZERO .
It is only possible to query
changes made to rounding mode
using fegetround
and FLT_ROUNDS ,
round_style
does not reflect changes
made by fesetround.
Not everything is affected by
setting the rounding mode .
#include <iostream>
#include <cfenv>
#include <cmath>
#include <cfloat>
#include <limits>
int main (void ){
std ::cout <<std ::boolalpha <<std ::hexfloat;
/* Set output format for boolean to print
true and false , and for float to
hex float */
std ::cout <<"FE_TONEAREST : "
<<(fegetround ( ) == FE_TONEAREST ) <<std ::endl;
/* Output :
FE_TONEAREST : true */
std ::cout <<"0x1.000000p+0f : " <<0x1.000000p+0f <<std ::endl;
/* 1.0000 0000 0000 0000 0000 000 0
when rounding to nearest , will
round to
1.0000 0000 0000 0000 0000 000
Output :
0x1.000000p+0f : 0x1p+0 */
std ::cout <<"0x1.000001p+0f : " <<0x1.000001p+0f <<std ::endl;
/* 1.0000 0000 0000 0000 0000 000 1
when rounding to nearest , will
round to
1.0000 0000 0000 0000 0000 000
since
1.0000 0000 0000 0000 0000 000 1
is haflway between
1.0000 0000 0000 0000 0000 000
and
1.0000 0000 0000 0000 0000 001
rounding to nearest will round to
the even
choice which is
1.0000 0000 0000 0000 0000 000
Output :
0x1.000001p+0f : 0x1p+0 */
std ::cout <<"0x1.000002p+0f : " <<0x1.000002p+0f <<std ::endl;
/* 1.0000 0000 0000 0000 0000 001 0
when rounding to nearest will
round to
1.0000 0000 0000 0000 0000 001
Output :
0x1.000002p+0f : 0x1.000002p+0 */
std ::cout <<"0x1.000003p+0f : " <<0x1.000003p+0f <<std ::endl;
/* 1.0000 0000 0000 0000 0000 001 1
is haflway between
1.0000 0000 0000 0000 0000 001
and
1.0000 0000 0000 0000 0000 010
, hence rounding
to nearest will round to the even
choice , which is
1.0000 0000 0000 0000 0000 010
Output :
0x1.000003p+0f : 0x1.000004p+0 */
std ::cout <<std ::defaultfloat;
/* Set output format for float to be
defaultfloat */
std ::cout <<"round (1.5 ) : " <<round (1.5 ) <<std ::endl;
/* Rounding mode is FE_TONEAREST ,
round is not affected by the
rounding mode set by fesetround .
Output
round (1.5 ) : 2 */
std ::cout <<"rint (1.5 ) : " <<rint (1.5 ) <<std ::endl;
/* Rounding mode is FE_TONEAREST ,
rint is affected by the rounding
mode set by fesetround .
Output
rint (1.5 ) : 2 */
std ::cout <<"round (-1.5 ) : " <<round (-1.5 ) <<std ::endl;
/* Output
round (-1.5 ) : -2 */
std ::cout <<"rint (-1.5 ) : " <<rint (-1.5 ) <<std ::endl <<std ::endl;
/* Output
rint (-1.5 ) : -2 */
std ::fesetround (FE_DOWNWARD );
/* Set rounding mode to downward ,
towards negative infinity */
std ::cout <<"FE_DONWARD : "
<<(fegetround ( ) == FE_DOWNWARD ) <<std ::endl;
/* Output :
FE_DONWARD : true */
std ::cout <<"FLT_ROUNDS towards negative infinity : "
<<(FLT_ROUNDS == 3 )
<<std ::endl;
/*Output
FLT_ROUNDS towards negative infinity : true */
std ::cout <<"round_style round to nearest : "
<<(std ::numeric_limits <double > ::round_style == 1 )
<<std ::endl;
/* round_style , does not reflect changes
made to rounding mode by fesetround
, hence this will output :
round_style round to nearest : true */
std ::cout <<std ::hexfloat;
/* Set output format for float to be
hex float */
std ::cout <<"0x1.000003p+0f : " <<0x1.000003p+0f <<std ::endl;
/* Output :
0x1.000003p+0f : 0x1.000004p+0 */
std ::cout <<std ::defaultfloat;
/* Set output format for float to be
defaultfloat */
std ::cout <<"round (1.5 ) : " <<round (1.5 ) <<std ::endl;
/* Rounding mode is FE_DONWARD
Output :
round (1.5 ) : 2 */
std ::cout <<"rint (1.5 ) : " <<rint (1.5 ) <<std ::endl;
/* Rounding mode is FE_DONWARD
Output :
rint (1.5 ) : 1 */
std ::cout <<"round (-1.5 ) : " <<round (-1.5 ) <<std ::endl;
/* Rounding mode is FE_DONWARD
Output :
round (-1.5 ) : -2 */
std ::cout <<"rint (-1.5 ) : " <<rint (-1.5 ) <<std ::endl <<std ::endl;
/* Rounding mode is FE_DONWARD
Output :
rint (-1.5 ) : -2 */
std ::fesetround (FE_UPWARD );
/* Set rounding mode to be upward
towards infinity */
std ::cout <<"FE_UPWARD : "
<<(fegetround ( ) == FE_UPWARD ) << std ::endl;
/* Output :
FE_UPWARD : true */
std ::cout <<std ::hexfloat;
/* Set output format for floating
points to hexfloat */
std ::cout <<"0x1.000003p+0f : " <<0x1.000003p+0f <<std ::endl;
/* Output
0x1.000003p+0f : 0x1.000004p+0 */
std ::cout << std::defaultfloat;
/* Set output format for floating points
to defaultfloat */
std ::cout <<"round (1.5 ) : " <<round (1.5 ) <<std ::endl;
/* Rounding mode is FE_UPWARD
Output :
round (1.5 ) : 2 */
std ::cout << "rint (1.5 ) : " << rint (1.5 ) << std ::endl;
/* Rounding mode is FE_UPWARD
Output :
rint (1.5 ) : 2 .*/
std ::cout << "round (-1.5 ) : " << round (-1.5 ) << std ::endl;
/* Rounding mode is FE_UPWARD
Output :
round (-1.5 ) : -2 */
std ::cout << "rint (-1.5 ) : " << rint (-1.5 ) << std ::endl <<std ::endl;
/* Rounding mode is FE_UPWARD
Output :
rint (-1.5 ) : -1 */
std ::fesetround (FE_TOWARDZERO );
/* Set rounding mode to downward
towards 0 */
std ::cout <<"FE_TOWARDZERO : "
<<(fegetround ( ) == FE_TOWARDZERO ) <<std ::endl;
/* Output :
FE_TOWARDZERO : true */
std ::cout <<std ::hexfloat;
/* Set floating point output format
to hexfloat */
std ::cout <<"0x1.000003p+0f : " <<0x1.000003p+0f <<std ::endl;
/* Output :
0x1.000003p+0f : 0x1.000004p+0 */
std ::cout <<std ::defaultfloat;
/* Set floating point output format
to defaultfloat */
std ::cout <<"round (1.5 ) : " <<round (1.5 ) <<std ::endl;
/* Rounding mode is FE_TOWARDZERO
Output :
round (1.5 ) : 2 */
std ::cout <<"rint (1.5 ) : " <<rint (1.5 ) <<std ::endl;
/* Rounding mode is FE_TOWARDZERO
Output
rint (1.5 ) : 1 */
std ::cout << "round (-1.5 ) : " << round (-1.5 ) << std ::endl;
/* Rounding mode is FE_TOWARDZERO
Output
round (-1.5 ) : -2 */
std ::cout << "rint (-1.5 ) : " <<rint (-1.5 ) <<std ::endl <<std ::endl;
/* Rounding mode is FE_TOWARDZERO
Output
rint (-1.5 ) : -1 */ }
The header
numbers
was defined , as part
of the C++20
standard . The C++
20 standard ,
also introduces the concept
of modules . Hence
with C++ 20
instead of using
#include ,
as in #include <numbers>
to include a header , one can use
import as in
import <numbers>; ,
to import modules .
The
header numbers ,
just
define some mathematical
constants
, which can be useful ,
such as pi , or
Euler's number e .
The type of these constant
is double , but
there is a template version
of these constants ending with
_v , such as
pi_v or e_v .
#include <iostream>
#include <numbers>
/* In C++20 , one can use
import <numbers>;
as of march 2021 ,
it is not working yet .*/
int main (void ){
std ::cout <<std ::numbers ::pi
<<" : Pi as double"
<<std ::endl;
/* Output :
3.14159 : Pi as double */
std ::cout <<std ::numbers ::pi_v <long double >
<<" : Pi as long double"
<<std ::endl;
/* Output :
3.14159 : Pi as long double */
std ::cout <<std ::numbers ::sqrt2
<<" : square root of 2"
<<std ::endl;
/* Output :
1.41421 : square root of 2 */
std ::cout <<std ::numbers ::e
<<" : Euler's number"
<<std ::endl;
/* Output :
2.71828 : Euler's number */
std ::cout <<std ::numbers ::ln2
<<" : ln(2)"
<<std ::endl;
/* Output :
0.693147 : ln(2) */
std ::cout <<std ::numbers ::log2e
<<" : log2(e)"
<<std ::endl;
/* Output :
1.4427 : log2(e) */
std ::cout <<std ::numbers ::log10e
<<" : log10(e)"
<<std ::endl;
/* Output :
0.434294 : log10(e) */ }
cin from the
standard library header
iostream , and
scanf
from the standard library header
cstdio ,
can be used for reading floating point numbers .
scanf
uses format specifiers to read data .
%f is used to read a
float , %lf
to read a
double where
l must be the
smallcase ,
%Lf is used
to read a long double , where
L must be capitalcase .
scanf reads floating point numbers
written in both the regular and scientific format .
#include <cstdio>
int main(void ){
float var_f { }; /* Initialize var_f to 0.0f */
double var_d { }; /* Initialize var_d to 0.0 */
long double var_lf { }; /* Initialize var_lf to 0.0l */
printf ("Enter a float : " );
scanf ("%f" , &var_f );
/* Read a float using %f format
specifier .*/
printf ("var_f is : %f \n" , var_f );
/* Print var_f using %f modifier */
printf ("Enter a double : " );
scanf ("%lf" , &var_d );
/* Read a double using %lf format
specifier .*/
printf ("var_d is : %f \n" , var_d );
/* Print var_d using %f */
printf ("Enter a long double : " );
scanf ("%Lf" , &var_lf );
/* Read a double using %Lf format
specifier .*/
printf ("var_lf is : %Lf \n" , var_lf );
/* Print var_lf using %Lf */ }
/* Example of running the program :
Enter a float : nan
var_f is : nan
Enter a double : inf
var_d is : inf
Enter a long double : -1.3e+12
var_lf is : -1300000000000.000000 */
cin is type aware
,
hence it is not necessary to
use a format specifier . It
can read floating point
numbers , written in both
regular , and scientific format ,
but it does not identify the
special values inf ,
or NAN .
#include <iostream>
int main(void ){
using std ::cout;
using std ::cin;
using std ::endl;
float var_f { }; /* Initialize var_f to 0.0f */
double var_d { }; /* Initialize var_d to 0.0 */
long double var_lf { }; /* Initialize var_lf to 0.0l */
cout <<"Enter a float : ";
cin >>var_f;
/* cin is type aware , read a float
using cin .*/
cout <<"var_f is : " <<var_f <<endl;
/* Output var_f read value . */
cout <<"Enter a double : ";
cin >>var_d;
/* Read a double using cin .*/
cout <<"var_d is : " <<var_d <<endl;
/* Output the read value of var_d */
cout <<"Enter a long double : ";
cin >>var_lf;
/* Read a long double using cin .*/
cout <<"var_lf is : " <<var_lf <<endl;
/* Output the value of var_lf using
cout */ }
/* Example of running the program :
Enter a float : 1.3E-1
var_f is : 0.13
Enter a double : 1.3
var_d is : 1.3
Enter a long double : -1.4
var_lf is : -1.4 */
It
is possible to
get a floating point number from a string
, by using one of the string
header methods : stof ,
stod or stold .
#include <iostream>
#include <string>
int main (void ){
size_t numCharacters_Processed { };
/* initialize the number of characters
processed to 0 .*/
float var_f = std ::stof (" -inf" , &numCharacters_Processed );
/* Use stof , to get a float from a
string .
Pass the string to be converted ,
and the address of a variable , which
will be set to the number of characters
processed .
The same principle apply to stod
which gets a double , and stold
which gets a long double .*/
std ::cout <<var_f <<" : var_f , "
<<numCharacters_Processed <<" : characters processed \n";
/* Output :
-inf : var_f , 6 : characters processed */
numCharacters_Processed = 0;
double var_d = std ::stof ("1.0e12" , &numCharacters_Processed );
std ::cout <<var_d <<" : var_d , "
<<numCharacters_Processed <<" : characters processed \n";
/* Output :
1e+12 : var_d , 6 : characters processed */
numCharacters_Processed = 0;
long double var_ld = std ::stold ("nan" , &numCharacters_Processed );
std ::cout <<var_ld <<" : var_ld , "
<<numCharacters_Processed <<" : characters processed \n";
/* Output :
nan : var_ld , 3 : characters processed */ }
When
the result of a floating point operation is
NAN , which is not a number , then
arithmetic operations involving NAN ,
such as addition , or subtraction,
result in NAN .
Comparison
operations ,
such as < or == ,
involving NAN , yields false ,
even if comparing
NAN with NAN .
The only exception is != , which
always yields true ,
when comparing NAN
to anything , even itself .
NAN
can be gotten
, when dividing
0 by 0 ,
or when 0 is multiplied by
infinity , or when infinity is divided
by infinity , or when subtracting
infinities of the same sign , as in
positive infinity , from positive
infinity , or when adding infinities
of the opposite sign .
#include <iostream>
#include <cmath>
int main (void ){
using std ::cout;
cout << std ::boolalpha;
/* Set output for boolean
values to be alpha , which
is true and false .*/
cout <<(NAN + 1 ) << "\n";
/* Arithmetic operations involving NAN
results in NAN .
Output :
NAN */
cout <<(NAN == 0.0 / 0.0 ) <<"\n";
/* Comparison operations involving
NAN always yields false , except
for != which always yield true .
Output :
false */}
Infinty
can be gotten , when dividing
a non zero value by 0 ,
whereas dividing a number by infinity
yields 0 .
Adding infinities of the same sign or with a number ,
result in infinities
,
subtracting infinities of opposite sign or with
a number , result in infinities ,
multiplying
infinty by an infinity , or by
a number beside 0 ,
yields infinity , dividing an infinity
by a number , yields infinity .
#include <iostream>
#include <cmath>
int main (void ){
using std ::cout;
cout <<1 / 0.0 <<"\n";
/* Output :
inf */
cout <<(INFINITY + INFINITY ) <<"\n";
/* Output :
inf */
cout <<(1 / 0.0 - -1 / 0.0 ) <<"\n";
/* Output :
inf */
cout <<(INFINITY * INFINITY ) <<"\n";
/* Output :
inf */
cout <<(INFINITY / 0.0 ) <<"\n";
/* Output :
inf */ }